SECTION I
RESEARCH AND METHODOLOGIES

Short-term monitoring of benzene air concentration in an urban area: a preliminary study of application of Kruskal-Wallis non-parametric test to assess pollutant impact on global environment and indoor

Monitoraggio a breve termine delle concentrazioni di benzene in aria urbana: uno studio preliminare di applicazione del test Kruskall-Wallis per valutare l'impatto dell'inquinante sull'ambiente esterno ed interno

Maria Chiara Mura; Marco De Felice; Roberta Morlino; Sergio Fuselli

Dipartimento di Ambiente e Connessa Prevenzione Primaria, Istituto Superiore di Sanità, Rome, Italy

Address for correspondence

SUMMARY

In step with the need to develop statistical procedures to manage small-size environmental samples, in this work we have used concentration values of benzene (C6H6), concurrently detected by seven outdoor and indoor monitoring stations over 12 000 minutes, in order to assess the representativeness of collected data and the impact of the pollutant on indoor environment. Clearly, the former issue is strictly connected to sampling-site geometry, which proves critical to correctly retrieving information from analysis of pollutants of sanitary interest. Therefore, according to current criteria for network-planning, single stations have been interpreted as nodes of a set of adjoining triangles; then, a) node pairs have been taken into account in order to estimate pollutant stationarity on triangle sides, as well as b) node triplets, to statistically associate data from air-monitoring with the corresponding territory area, and c) node sextuplets, to assess the impact probability of the outdoor pollutant on indoor environment for each area. Distributions from the various node combinations are all non-Gaussian, in the consequently, Kruskal-Wallis (KW) non-parametric statistics has been exploited to test variability on continuous density function from each pair, triplet and sextuplet. Results from the above-mentioned statistical analysis have shown randomness of site selection, which has not allowed a reliable generalization of monitoring data to the entire selected territory, except for a single "forced" case (70%); most important, they suggest a possible procedure to optimize network design.

Key words: non-parametric statistics, Kruskall-Wallis test, air pollutant, sampling site selection, indoor/outdoor monitoring.

RIASSUNTO

In linea con l'operazione di trasferimento di procedure per il trattamento statistico di piccoli campioni ambientali, in questo lavoro utilizziamo i valori di concentrazione di benzene rilevato simultaneamente per 12 000 minuti in sette postazioni outdoor ed indoor, al fine di stabilire: la rappresentatività dei dati sul territorio e, successivamente, l'impatto dell'inquinante sull'ambiente interno. La rappresentatività sul territorio, come si sa, è legata alla geometria dei punti di rilevamento; questa è decisiva per la valutazione di un inquinante d'attenzione sanitaria quale quello utilizzato in questo lavoro. In base al principio di progettazioni delle reti di rilevamento, assumiamo, pertanto, le postazioni come nodi per configurare una rete di triangoli contigui; combiniamo, opportunamente, a: a) coppie le distribuzioni di inquinante, provenienti dai nodi che individuano i lati del triangoli, per stabilire la stazionarietà dell'inquinante su di essi; b) terne, per associare probabilisticamente la lettura del monitoraggio dell'inquinante alla corrispondente definita area territoriale; c) sestine per valutare su ogni area la probabilità d'impatto dell'inquinante outdoor sull'indoor. Trattandosi di piccoli campioni statistici, le distribuzioni sono di tipo non Gaussiano. Utilizziamo, pertanto, la statistica non parametrica di Kruskall-Wallis (KW) per testare la variabilità di ogni combinazione di coppie, terne e sestine di distribuzioni. I risultati ottenuti evidenziano: la casualità della allocazione delle postazioni che non permette di estendere al territorio, tranne che in un solo caso "forzato" (70%), la lettura del monitoraggio effettuato; più importante, individuano una possibile procedura per ottimizzare la rete.

Parole chiave: test non parametrico, Kruskall-Wallis test, inquinanti dell'aria, postazioni spaziali, indoor/outdoor monitoraggio.

INTRODUCTION

Reliability of environmental data monitoring is guaranteed by the correct functioning of sampling stations. An important example is represented by geodetic and pluviometric networks, as well as air quality ones, which are planned to assure reliable data from monitoring air quality and to allow making plausible predictions [1]. Both when planning and managing a network, analysis of variance for distributions of pollutants detected between two nodes plays a significant role in ruling out variability of the studied phenomenon along sides of network triangles [2]; in fact, the existence of variability would invalidate the allocation of sampling sites, so that data, suffering from error propagation, would not be representative of the pollution level over the selected area. Network planning and management often require a set of parametric techniques, which are usually applied to either retrieved or simulated pollutant time series; these ones constitute largescale databases characterized by Gaussian distributions. However, short-term monitoring campaigns generally produce non-Gaussian statistical distributions; this phenomenon can be already observed in graphical representation of data, which can be non-normal in some areas and, too, non-homoscedastic. Therefore, parametric statistical analysis cannot be used to design or test the allocation of survey stations of a network and, consequently, the extension of pollution data from single sites to the entire territory, both to assess outdoor and indoor environmental impact and risk, can prove difficult. In order to retrieve information from this type of campaigns, we have been exploiting statistical methods which are suitable for managing small-size samples [3-5]. Such methods are non-parametric [6-9] and are widely used in economics, biology, sociology etc. [10, 11], as well as, but to a much smaller extent, in the environmental context. A short-term benzene monitoring campaign, performed by means of seven indoor and outdoor stations, has allowed us to develop this application and to assess the allocation of sampling sites by evaluating outdoor data probabilities and the impact probability of this pollutant of sanitary interest on indoor environment. Kruskal-Wallis test, which we have successfully used in later studies, has been chosen to perform analysis of variance.

MATERIALS AND METHODS

Databases

Our database is the result of a monitoring of benzene concurrently performed inside and outside seven houses in a urban area over four consecutive intervals of 3000 minutes each. The sampling strategy implied the random choice of the urban areas where localizing the monitoring devices, "radiello", so to analyze the local pollution status. The amplitude of the consecutive monitoring intervals was set as a function of the analytical sensitivity of the monitoring procedure in terms of both estimated concentration variance and instrument sensitivity. We have 14 distributions at our disposal, each characterized by 4 values of pollutant mean concentration (Table 1).

Procedure

Network construction

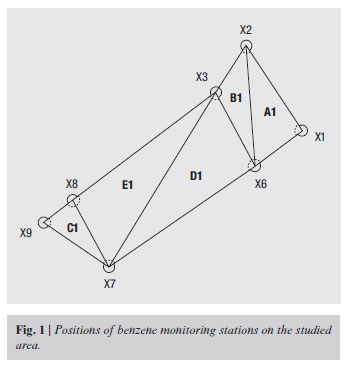
First, we have located each of the seven houses (I = 1 to 3 and 6 to 9) on the selected area and considered it as a node to design a hypothetical wired network made of triangles; in each vertex a sampling site. The first configuration comprises 5 wires:

These 5 triangles are adjoining if taken in the following order: A1, B1, D1, E1, C1, A1, B1 and C1 are characterized by approximately equal areas, but much smaller than D1's and E1's, which are quite similar. The second configuration has been created just changing vertices of A1 and B1 triangles and it includes 2 wires:

A2+B2 occupies the same area as A1+B1.

The entire selected area is enclosed in a polygon having vertices at x1, x2, x3, x8, x9, x7 and x6 (Figure 1). Distances between single stations are shown in Table 4, column 2.

Construction of statistical samples

Samples have been created arranging distributions from vertices of each triangle in triplets (Table 1). Precisely, for the first configuration, five triplets for outdoor monitoring and five for outdoor/indoor one (10 combinations in all) have been obtained. For the second "trial" configuration on the same area, two triplets for outdoor monitoring have been generated. Pairs of distributions from triangle sides have been extracted from Table 1. Triangle sides, together with their lengths, for the first configuration are shown in Table 4, columns 1 and 2 respectively. All samples are small-size and statistically independent of each other. We checked the lack of between samples correlations by means of the application of Spearman's ρ ranks based correlation coefficient.

Non-parametric test

The chosen non-parametric technique has been KW test [12, 13]. It make use of ranks and is analogous to one-criterion ANOVA for parametric statistics. It has been used in order to establish whether pollutant distributions belong to the same population or not at the significance level α = 0.05.

KW test requires the transformation of concentration values into ranks for each node pair, triplet and sextuplet; this way, the parametric space is replaced by the non-parametric, a-dimensional one [3]. The transformation is performed on the continuous density function according to the following procedure:

Clearly, each concentration value can take on a different "weight" according to the configuration it is included in. For example, the transformation of benzene mean-concentration values into ranks for indoor/outdoor monitoring in A1 area over four consecutive time intervals of 3000 minutes is shown in Table 2.

Some trends for triplet rank-distributions from outdoor monitoring are shown in Figure 2 with reference to A1; Figure 3 to B1; each graph contains ranks from a triplet distribution - for each (outdoor) station in the selected triangle, ranks calculated over each of the four time intervals are shown. This graphical criterion allows identifying possible space trends in the studied phenomenon starting from its components.

KW null hypothesis (H₀) postulates no differences exist between studied distributions (i.e., they are stationary) at the significance level α < = 0.05. If the work hypothesis consists in expecting to find variability, H₀ is rejected when H-value, which is computed by:

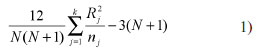
where:

is larger than χ²-value at the significance level α = 0.05 on the table of critical values of chi-square distribution [5]. On this table, a row corresponding to the number of k-1, which returns the number of degrees of freedom, is selected, in search for the larger χ²-value which is smaller than H. The corresponding column-value determines if a significant non-random difference exists between distributions. In case of tied values, a correction factor:

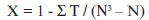
where T = t³ - t with t corresponding to the number of ex-aequo observations in each group and N to the total number of samples (1).

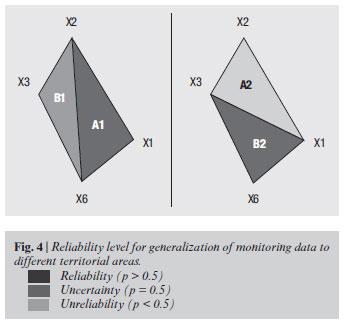
Kruskal-Wallis statistics is approximately distributed as a true χ²-one [14, 15]. If compared to Fisher's test, its power is about 3/π = 95.5% and increases at increasing of the number of observations on equal sampling intervals. KW test, which represents an extension of the median test, allows to define three probability (and, thus, reliability) levels to be associated to data. For triangle areas (triplets):

RESULTS AND DISCUSSION

Empirical analysis of graphs for triplets and sextuplets identifies a common variable structure in the space trend of the pollution phenomenon. Indeed, in the passage from ranks from one station to those from another one in the same wire a peculiar trend reversal is evident. In Figure 2, for instance, clear reversal can be identified for distributions from x2 station. Trend reversals are related to x2 and x3 stations in B1 (Figure 3). Anyway, in all graphs a space variability for the pollution phenomenon can be identified, which could be reasonably ascribed to chance. KW test, in its inferential form, underestimates this variability, since null hypothesis can never be rejected. Nevertheless, none of H-values corresponds to such a high probability to allow a 90% reliable generalization of monitoring data to network wires. Probability ranges corresponding to the computed H-values allow for a "conventional" statistical reading of pollutant concentrations on each triangular wire (Table 3). When forcing the reading of H-values, a 70% reliability in A1 area can be identified as the best (but relative) datum; the generalization of benzene impact on indoor environment in A1 can be obtained with the same reliability level (Table 4). For B1 area, the reading of outdoor data is uncertain, but a very good probability level (90%) is found as to benzene impact on indoor environment, which could be reasonably explained in terms of indoor more persistent concentration values due to residents' habits. Conversely, both parameters are unreliable for C1, D1 and E1 triangles. As to "trial" configurations, the reading of C₆H₆ outdoor data proves unreliable (30%) in A2 area (approximately equal to A1), while it becomes reliable (70%) in B2 ( B1). The reading of monitoring data shows a large range of error in this case, too. Therefore, the original configurations (A1 and B1) are to be preferred, since the reading is unreliable in neither wire. Results from KW test, applied to triangle sides, partly explain why the generalization of monitoring data is unreliable, except for the "forced" case corresponding to A1 triangle. The situation shown in Table 4, column 6, ranges from "stationarity" to "variability", up to test rejection (p = 0.05) in two cases corresponding to D1 and E1 triangle sides. Along x3-x7, x3-x8 and x6-x7 sides, pollutant distributions belong to different statistical populations and show very high dispersions; therefore, monitoring data suffer from significant signal propagation errors. One thing to be noted is that lengths of triangle sides selected by x3, x7 and x8 stations are larger than 1.5 km. Moreover side lengths in D1 and E1 wires are not homogeneous; for example, x3-x6 side (stationary condition) in D1 triangle is shorter than the other two ones (5% variability) by one third. Such a situation explains unreliability of data from these two network wires. A stationary condition cannot be identified between much closer stations either, such as x1-x6 and x2-x6 sides of A1 triangle. Moreover, the latter side corresponds to p = 0.5 (i.e., 50% instability), while x3-x6 side of B1 and D1 triangles is characterized by p = 0.7 (stationary condition), even though both sides have equal lengths (0.69 km). This confirms that probability levels found along wire sides are not influenced by distance between survey stations only; indeed, inhomogeneity in side lengths, generating different angle sizes, is a crucial factor, too (Figure 1). High stationarity is found along x1-x2 side of A1 triangle (99%) and x7-x8 side of C1 wire (90%); however, once again high variability along C1's other two sides does not allow a generalization of monitoring data to the entire area. An analogous, but much less marked and damaging situation exists in the case of A1 wire, whose distributions cannot be clearly attributed either to the same statistical population or to two different ones. Probability data for A1's, B1's and C1's sides, corresponding to a reliable, uncertain and unreliable condition respectively.

CONCLUSIONS

Sampling-site allocation represents a critical factor in obtaining reliable data on territorial basis, either for monitoring of benzene or of any other pollutant.

The above results come from the application of KW test to the pollutants concentration in urban sampling sites. These sites were used for simulating on hypothetical recording network. Only in one case, point based estimation not taking into account the recording network can be considered as "borderline relevant" for the entire territory, while in the other cases, being the point estimates largely affected by boundary conditions they did not allow for a reliable pollution estimation. KW test, which was chosen since available statistical samples were small-size, proved a suitable method for identifying network noise, which stands comparison with parametric techniques usually exploited in analyzing samples from fixed air-quality monitoring networks.

A further interesting application could be KW testing of this latter kind of samples; clearly, smallsize samples should be extracted, in this case, from the huge amount of data typically produced by such networks. The construction of density functions is a simple task even without the aid of the automated calculation tools commercially available today. No doubt, the optimization, which is in progress, of the polygon enclosing the studied territory is more complex, even though necessary to design a correctly working network.

Aknowledgments

The authors are very grateful for the graphic layout of this work to Massimo Delle Femmine, moreover they want to thank anonymous referee for the useful suggestions.

Conflict of interest statement

There are no potential conflicts of interest or any financial or personal relationships with other people or organizations that could inappropriately bias conduct and findings of this study.

Cautionary Note

As for the statistical significance values reported in the tables it is worth noting that they refer to the tables of Yates corrected chisquare for small samples. From a purely mathematical point of view these values are correct for the analysed case but, the descriptive character of the proposed strategy (the non-parametric test is used as a non probabilistic index of degree of between samples homogeneity and not in the usual mode of "significance detection") makes this correctness point not so relevant. Moreover, the widespread use of automatic probability calculation by software that do not use the Yates correction, makes it very unpractical to refer to tables. The editorial board is convinced that end-users will find much more comfortable and efficient to use standard chi-square computations that, in addition, for values outside the significance range (high p correspondent to high homogeneity) are numerically more relevant than Yates tables that in turn, being based on discrete values, are grossly approximated in this range.

Enrico Alleva Editor-in-Chief
and one member of the Editorial Board

References

1. Cirillo M, Finzi G, Fortezza F, Mamolini G, Marani A, Mura MC, Tamponi M, Tirabassi T. Models for design and evaluation of air pollutants monitoring networks. Roma: Istituto Superiore di Sanità; 1990. (Rapporti ISTISAN, 90/32).         

2. Singer I. Best approximation in normed linear spaces by elements of linear subspaces. New York -Heidelberg -Berlin: Springer-Verlag; 1970.         

3. Mura MC. Simplified reading of one-year air pollution. Ranking of chemical and physical variables. In: Borrego CA, Brebbia CA (Eds). Air Pollution XV. UK: WIT; 2007. p. 181-9.         

4. Mura MC, Falleni F, Jamja GM, Valero F. A scatter plot and 9. QQ plot qualitative analysis for the assessment of tropospheric ozone by a surface urban station. Boll Geof 1999;22(1-2): 61-70.         

5. Mura MC. A miscellany of statistical methods in analyzing tropospheric-ozone behavior related to wind direction in background and urban stations. In: Accademia Nazionale dei Lincei. Il buco dell'ozono: evoluzione e problemi radiativi. Atti dei convegni dei Lincei 245. Roma: Bardi Editore; 2009. p. 105-11.         

6. Siegel S, Castellan jr NJ. Non parametric statistics: for the behavioral science. New York: Mc Graw-Hill Book Company; 1956.         

7. Kruskal WH. Taking data seriously. In: Elkana Y, Lederberg J, Merton RK, Thackray A, Zurkerman H (Eds). Toward a metric of science: the advent of science indicators. New York: Wiley; 1978. p. 139-69.         

8. Kruskal WH. A non-parametric test for several sample problem. Ann Math Stat 1952;23:525-40.         

9. Kruskal WH. Criteria for judging statistical graphics. Utilitas Math 1982;21B:283-310.         

10. Anirvan Banerji. Economic Cycle Research Institute. The lead profile and other non-parametric tools to evaluate survey series as leading indicators. In: 24^th CIRET Conference. Wellington, New Zealand, March 17-20, 1999.         

11. Moore GH, Wallis WA. Time series significance tests based on signs of differences. J Amer Statist 1943;38:153-64.         

12. Kruskal WH, Wallis WA. Errata to use of ranks in one-criterion variance analysis. Jour Am Stat Assoc 1982;48:907-11.         

13. Wallace DL. Simplified beta-approximations to the Kruskal-Wallis H test. Jour Am Stat Assoc 1959;54:225-30.         

14. Andrews FC. Asymptotic behavior of some rank tests for analysis of variance. Ann Math Stat 1954;25:724-36.         

15. Cochran WG. The χ² test of goodness of fit. Ann Math Sta 1952; 23:315-45.         

Address for correspondence:
Maria Chiara Mura
Dipartimento di Ambiente e Connessa Prevenzione Primaria, Istituto Superiore di Sanità
Viale Regina Elena 299
0161 Rome, Italy
E-mail: mariachiara.mura@iss.it

Received on 4 June 2009.
Accepted on 30 March 2010.