THEME PAPERS
Socioeconomic inequalities in child mortality: comparisons across nine developing countries
Inégalités socio-économiques et mortalité infantile : comparaisons dans neuf pays en développement
Desigualdades socioeconómicas y mortalidad infantil: comparación de nueve países en desarrollo
Adam Wagstaff1
Development Economics Research Group and Human Development Network, The World Bank, 1818 H Street NW, Washington, DC, 20433, USA (e-mail: awagstaff@worldbank.org); and School of Social Sciences, University of Sussex, Brighton, England
ABSTRACT
This paper generates and analyses survey data on inequalities in mortality among infants and children aged under five years by consumption in Brazil, Côte dIvoire, Ghana, Nepal, Nicaragua, Pakistan, the Philippines, South Africa, and Viet Nam. The data were obtained from the Living Standards Measurement Study and the Cebu Longitudinal Health and Nutrition Survey. Mortality rates were estimated directly where complete fertility histories were available and indirectly otherwise. Mortality distributions were compared between countries by means of concentration curves and concentration indices: dominance checks were carried out for all pairwise intercountry comparisons; standard errors were calculated for the concentration indices; and tests of intercountry differences in inequality were performed.
Keywords: developing countries; health services accessibility; infant mortality; living conditions; social justice; socioeconomic factors.
RÉSUMÉ
Lamélioration de la santé des pauvres est devenue un but pour un certain nombre dorganisations internationales, et notamment la Banque mondiale et lOMS, ainsi que pour les pouvoirs publics de plusieurs pays dans le cadre de leurs politiques nationales et de leurs programmes daide au développement. Ce but reste difficile à atteindre dans la mesure où les données sur lampleur et les causes des inégalités de santé font défaut, en particulier dans les pays en développement. Le présent article a pour objectif de combler cette lacune en fournissant des éléments dinformation à la fois sur lamplitude et sur les causes des inégalités de mortalité dans un sous-groupe de la population des pays en développement, à savoir lenfant de moins de cinq ans.
Larticle commence par la description des méthodes de mesure appliquées à létendue des inégalités de la mortalité infanto-juvénile dans les différentes classes économiques et à la recherche décarts significatifs entre les pays. Ces méthodes consistent à construire des courbes de concentration donnant le pourcentage cumulé de décès pour la classe dâge étudiée pendant la période de référence en fonction du pourcentage cumulé denfants nés vivants rangés en fonction de leur situation économique. Les courbes situées bien au-dessus de la diagonale, laquelle représente la ligne dégalité, indiquent une distribution très inégale de la mortalité avec la classe économique, les décès étant concentrés parmi les plus démunis. Lindice de concentration (égal à deux fois laire comprise entre la courbe de concentration et la diagonale) est une mesure de linégalité; il prend une valeur négative lorsque les décès sont concentrés parmi les plus pauvres. Nous indiquons un estimateur qui permet de calculer une erreur type de cet indice et, par conséquent, de procéder à des tests de signification.
Ces méthodes ont été appliquées aux pays suivants : Afrique du Sud, Brésil, Côte dIvoire, Ghana, Népal, Nicaragua, Pakistan, Philippines et Viet Nam. Les données utilisées sont celles de létude sur la mesure des niveaux de vie réalisée par la Banque mondiale, sauf dans le cas des Philippines où les données proviennent de lenquête longitudinale sur la santé et la nutrition de 1991 conduite dans lîle de Cebu. Les taux de mortalité moyens des échantillons calculés avec les données étaient assez proches de ceux obtenus par dautres sources, et les erreurs types relatives se situaient dans des limites considérées comme acceptables. Les inégalités de mortalité des moins de cinq ans étaient supérieures aux inégalités de mortalité infantile, particulièrement élevées au Brésil, et assez élevées au Nicaragua et aux Philippines. Les inégalités de mortalité chez les moins de cinq ans étaient inférieures en Afrique du Sud, en Côte dIvoire et au Népal, tout en étant plus élevées quau Ghana, au Pakistan et au Viet Nam.
RESUMEN
La mejora de la salud de la población pobre se ha convertido en un objetivo de varias organizaciones internacionales, incluidos el Banco Mundial y la OMS, así como de varios gobiernos nacionales en el marco de sus políticas internas y sus programas de asistencia para el desarrollo. Las actividades encaminadas a ese objetivo se ven dificultadas por la escasez de datos sobre la magnitud y las causas de las desigualdades en salud, sobre todo en los países en desarrollo. En el presente artículo se ha intentado colmar esa laguna generando pruebas científicas sobre la magnitud y las causas de las desigualdades en materia de mortalidad en un sector de la población del mundo en desarrollo, a saber, los niños menores de cinco años.
El artículo empieza exponiendo sucintamente los métodos disponibles para medir la magnitud de las desigualdades en materia de mortalidad infantil entre distintos grupos económicos y para analizar la significación de las diferencias entre países. Para ello se elaboran curvas de concentración de los porcentajes acumulativos de defunciones para el grupo de edad en cuestión a lo largo del periodo de referencia frente a los porcentajes acumulativos de niños nacidos, ordenados conforme a su situación económica. Las curvas situadas muy por encima de la diagonal, que corresponde a la línea de igualdad, reflejan una muy desigual distribución de la mortalidad entre los grupos económicos, con las defunciones concentradas entre los más desfavorecidos. El índice de concentración (el doble del área delimitada por la curva de concentración y la diagonal) es una medida de la desigualdad, y tiene valor negativo cuando las defunciones se concentran entre las clases bajas. Se presenta un estimador que permite calcular el error estándar de ese índice, y someterlo así a pruebas de significación.
Estos métodos se aplicaron a los siguientes países: Brasil, Côte dIvoire, Ghana, Nepal, Nicaragua. Pakistán, Filipinas, Sudáfrica y Viet Nam. Se emplearon datos del estudio de medición de los niveles de vida del Banco Mundial, excepto en el caso de Filipinas, país para el cual se recurrió al estudio longitudinal sobre salud y nutrición realizado en Cebu en 1991. Los cálculos arrojaron tasas de mortalidad promedio muestrales razonablemente próximas a las de otras fuentes, con errores estándar relativos que estaban dentro de los límites admisibles. Las desigualdades observadas en la mortalidad de menores de cinco años fueron superiores a las correspondientes a la mortalidad de lactantes, y resultaron ser muy pronunciadas en el Brasil, y relativamente altas en Nicaragua y Filipinas. Las desigualdades de mortalidad de los menores de cinco años fueron inferiores en Côte dIvoire, Nepal y Sudáfrica, y aún menores en Ghana, el Pakistán y Viet Nam.
Introduction
Improving the health of the poor and reducing health inequalities between the poor and non-poor have become central goals of certain international organizations, including the World Bank and WHO, as well as of several national governments in the contexts of their domestic policies and development assistance programmes.a Since 1997, the World Banks top priority in its health, nutrition and population sector has been "to work with countries to improve the health, nutrition, and population outcomes of the worlds poor, and to protect the population from the impoverishing effects of illness, malnutrition and high fertility" (1). Reducing the disease burden of the poor is now WHOs first priority (2). The United Kingdom is committed to reducing health inequalities within its borders and has made improving the health of the poor the key objective of its health work in the developing world. Other European countries, especially the Netherlands and Sweden, have either committed themselves to reducing health inequalities domestically or have shown considerable interest in work on health inequalities.
Efforts to achieve these goals are hampered by, inter alia, a shortage of comparable data on health levels among the poor and on inequalities in health between the poor and non-poor, especially in developing countries. Extensive data are available on population, i.e. average, health outcomes for most countries. Disaggregated data are available for a number of dimensions such as regions, educational levels, and occupations in industrialized countries, but there have been comparatively few studies relating to the developing world. However, the disaggregated data are not typically comparable across countries or over time, and in any case do not shed light directly on gaps between the poor and non-poor. Surprisingly few data are available on health outcomes by income or consumption,b and the disaggregated data that do exist are rarely expressed in the form of a summary index that would allow temporal or between-country comparisons.c Consequently, little is known about how countries compare in terms of income-related health inequalities or about how specific countries have fared over time.
The present paper aims to diminish this information gap by:
outlining methods of measuring health inequalities between the poor and non-poor and of testing for significant differences across countries or temporal changes;
generating evidence on the magnitude of inequalities between the poor and non-poor in a particular dimension of health, namely mortality, and in a particular section of the population of the developing world, namely children aged under five years.
It is hoped that the methods will be useful in future work aiming to compare countries or monitor trends. The methods are applied to nine developing countries: Brazil, Côte dIvoire, Ghana, Nepal, Nicaragua, Pakistan, the Philippines, South Africa, and Viet Nam. Jamaica and Romania were originally considered but were excluded because surveys produced mortality estimates that differed excessively from published values. The data used, with the exception of those for the Philippines, were taken from the World Banks Living Standards Measurement Study (LSMS).d The data for the Philippines relate to the 1991 sweep of the Cebu Longitudinal Health and Nutrition Survey.d It is also hoped that the results will stimulate research into what accounts for the observed between-country differences in inequalities between the poor and non-poor under-five mortality rates, with a view to throwing light on what configuration of policies makes for low average rates and low inequalities.
Mortality rates at early ages have an important bearing on life expectancy at birth, a key health indicator. Indeed, infant and under-five mortality are seen as key health indicators in their own right. Furthermore, mortality data are relatively hard (4)e, whereas morbidity data may well be perceived differently by different economic groups and may consequently be subject to reporting bias.
The choice of the LSMS as the database needs some explanation. In two key respects it is not ideal for the task: the sample size in some of the surveys is relatively small, which could create problems, especially in low-fertility countries; and the fertility histories of some of the LSMS surveys are incomplete and permit only indirect estimates of mortality rates.f
In both respects, LSMS surveys are inferior to the typical demographic and health survey (DHS), which uses a large sample and invariably contains complete fertility histories, thereby allowing direct mortality estimates to be obtained. Unfortunately, however, in almost all countries the DHS does not collect information on household income, consumption or expenditure, whereas the LSMS does. Data on expenditure, income and household production have been combined by the World Bank to give a measure of household consumption, which is considered by poverty specialists to provide a far better indicator of living standards than traditional income data. In this respect the LSMS is distinctly superior to the DHS.g
Measuring and testing for inequalities in mortality
Let us assume that we have a variable capturing the economic status of households. We rank children born alive according to their households economic status and divide the sample into quintiles. In principle, deciles could be used, but most LSMS surveys are too small to make such a fine classification meaningful (6). We then estimate infant and under-five mortality rates for each quintile.
In Fig. 1, L(p) is a mortality concentration curve, showing the cumulative proportion of deaths (on the y-axis) against the cumulative proportion of children at risk (on the x-axis), ranked by living standards and beginning with the most disadvantaged child. The similarity with the Lorenz curve is obvious, but one should bear in mind that we are not ranking by the variable whose distribution we are investigating. Rather, we are looking at the distribution of mortality, not across quintiles grouped by mortality but rather across quintiles grouped by economic status. If L(p) coincides with the diagonal, all children, irrespective of their economic status, enjoy the same mortality rates. If, as is more likely the case, L(p) lies above the diagonal, inequalities in mortality favour the better-off children; we shall call such inequalities pro-rich. If L(p) lies below the diagonal, we have pro-poor inequalities in mortality (inequalities to the disadvantage of the better-off). The further L(p) lies from the diagonal, the greater the degree of inequality in mortality across quintiles of economic status. If L(p) of country X is everywhere closer to the diagonal than that of country Y, then country Xs concentration curve is said to dominate that of country Y. It seems reasonable to conclude that there is unambiguously less inequality in mortality in country X than in country Y.
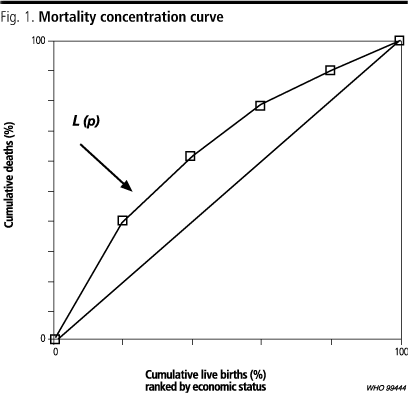
Where concentration curves cross or where a numerical measure of health inequality is required, the concentration index can be used. It is denoted below by C and is defined as twice the area between L(p) and the diagonal. This index is related to the relative index of inequality (RII) (7), which is used extensively by epidemiologists and others in analyses of socioeconomic inequalities in health and mortality (8). C is zero when L(p) coincides with the diagonal, negative when L(p) lies above the diagonal, and positive when L(p) lies below the diagonal. In general, with T economic groups, C can be expressedh as

where 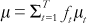 is the overall mean mortality rate,mt is the rate of the tth economic group, and Rt is its relative rank, defined as
is the overall mean mortality rate,mt is the rate of the tth economic group, and Rt is its relative rank, defined as

and indicating the cumulative proportion of the population up to the midpoint of each group interval. Alternatively, C can be calculated from grouped data using the following convenient regression:
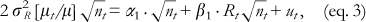
where 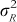 the variance of Rt, nt is the number of ever-born children in group t, a1 and b1 are coefficients, and ut is an error term. The estimator of b1 is equal to
the variance of Rt, nt is the number of ever-born children in group t, a1 and b1 are coefficients, and ut is an error term. The estimator of b1 is equal to
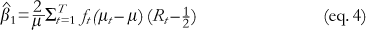
which, from eq. (1), shows that b1 is equal to C. Readers familiar with the RII will note that eq. (3) is essentially the same as the regression equation used to calculate this index when grouped data are used: the square roots of the group sizes transform the estimation from ordinary least squares to weighted least squares, and the division of the left-hand side by m simply means that the slope coefficient b1 is the RII rather than the slope index of inequality (SII). The only difference, then, between eq. (3) and that used to calculate the RII is that the left-hand side contains the variance of the rank variable. This, however, approaches 1/12 as the sample size grows, and can therefore be treated approximately as a constant across samples. Thus the RII and C ought to rank distributions the same there is little to choose between the two measurement approaches, although the concentration curve has the attraction of facilitating graphical comparisons of health inequalities.
When undertaking intercountry or temporal comparisons, one needs to bear in mind that the mortality rates are derived from survey data and are therefore subject to sampling variation. It is useful, therefore, to couple numerical comparisons of the index C with tests to assess the statistical significance of any intercountry or temporal differences. An attraction of the convenient regression (eq. (3)) is that it provides a standard error for the concentration index C. This standard error is not, however, wholly accurate, since the observations in each regression equation are not independent of one another because of the nature of the Rt variable. The following standard error estimator (6) takes into account the serial correlation in the data:
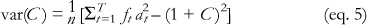
where

and

is the ordinate of L(s), with qo = 0. It is this estimator that is used, rather than the one in eq. (3), which is used in the section below dealing with levels and inequalities in childhood mortality.
Data and variable definitions
The surveys used in the present paper are listed in Table 1. They vary in sample size (1600 to 8848 households), timing (spanning the period 198796) and mortality information (two contain incomplete fertility histories and hence permit only indirect estimates of mortality). It should be noted that the geographical coverage of the Brazil and Philippines surveys was limited.
Measurement of living standards
Living standards were measured as equivalent household consumption on the survey date. Household consumption was measured using the constructed aggregate consumption variable in the LSMS surveys. Although the methodological details varied somewhat from survey to survey, the aim in each case was broadly the same: to arrive at a measure of household consumption of food, housing and other non-food items that reflected not only household outlays but also any household production of food and non-food items and the rental value of the home and other durables. The LSMS surveys were unique in the comprehensiveness with which living standards could be measured. In the case of the Cebu Longitudinal Health and Nutrition Survey, a broad measure of income was constructed, including wage and non-wage income, in-kind income received from non-family members, the value of home-grown vegetables and other produce, and the rental value of the family home and other consumer durables.
We equivalized household consumption to take into account differences in household size. The two extreme positions on equivalization are to assume that there are:
no economies of scale in household consumption (i.e. it costs two persons twice as much to live as one);
maximum economies of scale (i.e. two persons can live as cheaply as one).
These and certain intermediate positions can be represented by the following relationship between equivalent consumption and actual consumption:

where E is equivalent consumption, A is actual consumption, H is household size, and e is an equivalence scale elasticity (9). On the assumption that there no economies of scale, e is set equal to 1, and equivalent consumption is simply per capita consumption. On the assumption that two or more persons can live as cheaply as one, e is set equal to 0, and equivalent consumption is simply aggregate household consumption. Although it is not uncommon to find e set equal to 1 (the per capita adjustment), a more plausible position, at least in countries where a sizeable proportion of consumption is on non-food items, is that there are some economies of scale but that the elasticity e is positive. In OECD countries it was found that most equivalence scales could be approximated quite closely by eq.(8) and that, on average, the implied value of the elasticity e was around 0.4 (9). In Ecuador, Hentschel & Lanjouw (10) experimented with three values of e: 0.4, 0.6, and 1.0. In what follows we set e = 0.5; this seems to be a reasonable intermediate position. The per capita adjustment, i.e. with e = 1, tended to make the mortality inequalities smaller, and in the case of Pakistan the gradient was reversed.
Measurement of mortality
Where complete fertility histories were available, mortality rates were estimated using the direct method. This is illustrated in Table 2 with the data from the Cebu Longitudinal Health and Nutrition Survey. As in all the surveys that included complete fertility histories with the exception of Brazil, for which fertility histories for only the last five years were available only children born in the 10 years preceding the survey were included in the estimation of mortality rates. In the case of Cebu, this resulted in the selection of 6645 children. In Table 2, the first row of column 3 indicates how many of these were withdrawn from the life table through censoring during the first 6 months, this being the interval chosen for the life table. There were, in other words, 163 children of the 6645 who were born within the 6 months prior to the survey and who therefore had less than 6 months of exposure out of a possible maximum of 10 years. It was assumed that these 163 children were, on average, exposed for only half of the 6 months, so that the total number of children exposed during the first 6 months was 6645 less half of 163, i.e. 6564. (It is because of this assumption that the choice of interval width matters. The DHS results were obtained using non-fixed intervals, with smaller intervals for the first year of life than for later years. This, being computationally cumbersome, was not adopted in the present study. With regard to the fixed-width options, reducing the interval to less than half a year had little effect whereas choosing a longer interval made a considerable difference.)
Of the 6645 children born during the previous 10 years, 166 died during the first 6 months and the proportion surviving was therefore 6398/6564, i.e. 0.975. The mortality rate for the first 6 months, 0.5q0, was 1 0.975, i.e. 0.025. The number of children starting the second 6 months was 6645163166, i.e. 6316. Of these, 158 were exposed for less than 6 months, i.e. were born less than a year before the survey. Of the 6237 children exposed to the risk of death in their first year of life, 86 died before their first birthday, giving 0.961 as the cumulative proportion of children surviving from birth to their first birthday. Column 7 of Table 2 shows the survival function. From this we obtain an infant (i.e. under-1-year-old) mortality rate of 0.039, i.e. 39 per 1000 live births. Column 9 gives the standard error of the cumulative proportion surviving, or equivalently the standard error of the mortality rate from birth to the end of the interval in question. Column 10 expresses this as a proportion of the mortality rate. The final column shows the hazard rate, l (t) the rate at which the survival function, S(t), decreases over time, d ln S(t)/dt. Finally, the bottom row of column 8 gives the underfive mortality rate, 5q0, which in this case was 78 per 1000 live births, with a standard error of 4.5%.
In the cases where incomplete fertility histories were used, the mortality estimates were obtained by the indirect method (5). This involved superimposing on model life tables the data on live births and deaths.
The informational requirements for this were two-fold: the number of children ever born to the woman in question and the number of children who had died. Estimates can be obtained using the computer program QFIVE (5). The output included infant and under-five mortality estimates for women in different age bands for different regional life tables. The results reported elow are based on the regional life tables (Table 2) used by Hill & Yazbeck (11) for the countries in question. The rates reported are simple averages of the estimated rates for women in the age bands 2529 years, 3034 years and 3539 years.i
Levels and inequalities in childhood mortality in nine countries
It seems wise to start by comparing the aggregate mortality rates obtained from the surveys used here with the rates obtained from other surveys and sources for these countries.
Aggregate infant and childhood mortality rates from the surveys
Table 3 shows the infant and under-five mortality rates obtained from the surveys used in the present paper, along with standard errors where applicable. Also shown are the rates for the same periods calculated from the figures reported by Hill & Yazbeck (11). Where the direct method was used the sample average rates were, for the most part, reasonably close to these values, especially as regards under-five mortality. The relative standard errors were also encouraging the DHS typically reports standard errors of 48% (12). The exception was Brazil, where the direct mortality rate estimates were over 50% below the Hill & Yazbeck rates for the country as a whole, and where the standard errors were around 15% of the mortality rate. It should be noted that the survey used did not cover the whole of Brazil, while the Hill & Yazbeck figures were for the whole country. However, the exclusion of areas other than the south-east and north-east ought to result in a higher rather than a lower mortality rate (13). The indirect estimate for Brazil was marginally above the Hill & Yazbeck figure and hence the indirect method in this case seems a more reliable basis on which to investigate inequalities. The use of indirect estimates in the cases of Nicaragua and South Africa resulted in estimates deviating somewhat from the Hill & Yazbeck figures, although not dramatically. The aggregate results were thus encouraging and suggested that the LSMS data might reasonably be expected to shed some light on mortality differences related to economic status.
Differences by equivalent consumption in infant and under-five mortality
Table 4 shows the extent of inequalities in infant and under-five mortality. Except in Ghana, the poorest quintile suffered higher infant and under-five mortality rates than any other; in Ghana this was so for under-five mortality but not for infant mortality. In many countries there was a large gap between the bottom quintile and the rest of the population. This was especially true for under-five mortality, although there were exceptions, notably in Ghana, Pakistan and Viet Nam. Only in Brazil, Nicaragua, and the Philippines did the mortality rate decline monotonically with upward movement through the consumption distribution. This was true of South Africa for infant mortality but not for under-five mortality. In the other countries, except Pakistan, the corresponding trend was decidedly downward. Thus it appears that childhood survival prospects, at least in these countries, are worse for children born into poor families than for those born into better-off families, and that the prospects improve more or less steadily with upward movement through the income distribution.
It is not obvious from the data in Table 4 which countries have the greatest inequalities in infant and under-five mortality and which have the lowest. One complication is that the quintiles for Brazil, Nicaragua and South Africa relate not to children born but to mothers. It would be misleading, for example, to compare the bottom quintile for Brazil, which accounts for 34% of live births over the period in question, with that for Viet Nam, which accounts for 20%.
Inequalities in infant and under-five mortality: dominance checking
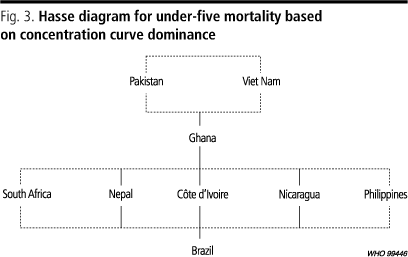
Inequalities in infant and under-five mortality can be circumvented by comparing concentration curves, i.e. undertaking a dominance-checking exercise. Concentration curves automatically attach the correct number of children to the mortality rate in question. In the case of infant mortality the picture was far from clear, with intersecting curves in a large fraction of the possible pairwise comparisons. The picture was clearer in the case of under-five mortality. Fig. 2 charts the deviations of the under-five mortality concentration curves from the 45º line. All concentration curves lie above the 45º line and hence above the horizontal axis in Fig. 2 indicating that pro-rich inequality in under-five mortality existed in all these countries. The concentration curve for Brazil lies the furthest from the 45º line by a long way and does not intersect with any of the other countries concentration curves. There is a group of countries with smaller inequalities and intersecting concentration curves in the middle of the chart Côte dIvoire, Nepal, Nicaragua, the Philippines, and South Africa. There are then three countries with far smaller inequalities Ghana, Pakistan and Viet Nam two of whose concentration curves intersect. These results can be represented by the Hasse diagram in Fig. 3. The countries on the same level, linked by broken lines, have intersecting concentration curves, while those further up have concentration curves lying closer to the 45º line and hence less inequality than those further down. Thus the concentration curves of Pakistan and Viet Nam dominate that of Ghana, which in turn dominates those of Côte dIvoire, Nepal, Nicaragua, the Philippines, and South Africa. In turn these countries concentration curves dominate the curve for Brazil.

Inequalities in infant and under-five mortality: concentration indices
An alternative approach is to calculate the concentration index measure of inequality. One reason for doing so is that the concentration curves give only a ranking, which in any case is incomplete. Fig. 2 and Fig. 3 reveal that Brazil has more inequality in under-five mortality than, say, the Philippines, but they do not indicate how much more. Fig. 3 puts Côte dIvoire on the same level as the Philippines, but from Fig. 2 it is clear that, although the concentration curves intersect, the Côte dIvoire curve is nearly always closer to the 45º line than that of Cebu. If we are prepared to accept the value judgements underlying the concentration index (like the Gini coefficient, the concentration index is most sensitive to transfers around the mean), the concentration index provides a means of comparing levels of inequality among countries with non-intersecting concentration curves, as well as acting as a tiebreaker in cases where the curves intersect. In addition, the concentration index lends itself straightforwardly to statistical testing by the methods outlined above. This allows us to explore the possibility that intercountry differences in inequality may be due to sampling variation. Methods for comparing the statistical significance of differences in concentration curve ordinates are available but their implementation is not straightforward.
Table 5 shows the concentration indices for the infant and under-five mortality data along with standard errors, computed using the accurate method outlined in eq. (5) above, and the corresponding t-values and 95% confidence intervals. Like the concentration curve, the concentration index takes into account the different numbers of children in the quintiles; this is important when comparing inequalities between countries where different methods have been used for estimating mortality. In all countries, inequalities in under-five mortality were more pronounced than inequalities in infant mortality. Indeed, in Côte dIvoire and Ghana the inequalities in under-five mortality were statistically significant, while those in infant mortality were not. In all the countries except Pakistan and Viet Nam the inequalities in under-five mortality were statistically significant, while in only five countries were inequalities in infant mortality significant. Among the countries with significant concentration indices there appeared to be substantial differences in levels of inequality. Brazil had by far the most unequal distributions of infant and under-five mortality, but Nicaragua, the Philippines, and South Africa also had fairly high levels of inequality in child survival across consumption groups. By contrast, Ghana had a very low level of inequality in under-five mortality, although it was statistically significant.
These apparent differences between countries raise the question as to which of the differences in inequality were statistically significant. Tables 6 and 7 give the results of t-tests indicating the significance of the differences between the concentration indices of the column and row countries. In Table 6, for example, Brazil has a greater level of inequality than Côte dIvoire (hence the minus sign in front of 1.92), but the difference between the two concentration indices was not statistically significant. Similarly, Brazils concentration index for infant mortality was larger in absolute size than Nicaraguas, but the difference was not significant. By contrast, Brazil had significantly higher inequalities in infant mortality than Ghana, Nepal, Pakistan, the Philippines, South Africa, and Viet Nam. The results of the t-tests for under-five mortality are summarized in a Hasse diagram (Fig. 4), where broken lines indicate a lack of significant difference and continuous lines indicate significance. Thus, there were no significant differences between the under-five mortality concentration indices of Ghana, Pakistan, and Viet Nam, nor between those of Côte dIvoire, Nepal, and South Africa, but the indices of the last three countries were significantly larger in absolute size than those of the first three. Brazil had significantly higher inequality in under-five mortality than the six countries above it in the Hasse diagram, but its concentration index was not significantly different from those of Nicaragua or the Philippines, whose indices, in turn, were not significantly different from those of Côte dIvoire, Nepal, and South Africa.
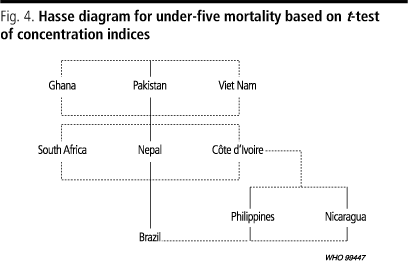
Although the Hasse diagrams (Figs. 3 and 4) are not identical, the broad conclusions are the same: Brazil has the most unequal distribution of under-five mortality by equivalent consumption and is followed very closely by Nicaragua and the Philippines; Côte dIvoire, Nepal, and South Africa have intermediate inequality levels; Ghana, Pakistan, and Viet Nam have low levels of inequality in under-five mortality.
Conclusions
The present paper outlines methods for measuring inequalities in health between the poor and non-poor and for testing the significance of differences or changes in these inequalities. The application of these methods to the measurement of inequalities in under-five mortality between the poor and non-poor produced a number of conclusions.
- The LSMS data gave tolerably good infant and under-five mortality estimates at the sample level, being relatively close to rates reported elsewhere and, in the case of the direct estimates, having relatively small standard errors. This was encouraging, since LSMS data have not always been perceived as useful for the estimation of childhood mortality.
- The application of concentration curves and indices to the data showed that inequalities in infant and under-five mortality were to the disadvantage of the worse-off. For the most part, these inequalities were statistically significant. More interestingly, the extent to which this was true varied between countries. Inequalities in under-five mortality were especially high in Brazil and rather high in Nicaragua and the Philippines. They were lower in Côte dIvoire, Nepal, and South Africa, but higher in these countries than in Ghana, Pakistan, and Viet Nam.
Certain areas outlined below have not been explored in the present study, and merit attention in the future.
- The results reflect a particular definition of living standards equivalent consumption, in which the number of equivalent adults is defined as the square root of the number of household members. This is not the only position that might be adopted, and different assumptions about the equivalence scale would produce different results. In Pakistan, for example, where the average household size is very large (over nine in the sample used in the present study), the choice of equivalence factor can have important implications for the results; moving to the per capita adjustment actually reverses the gradient in this case. The direction of impact is, of course, unpredictable, and could vary from one country to the next. Different rankings of countries could also be obtained if wealth or assets rather than consumption was considered and if other indicators, such as anthropometric measures, were considered.
- We investigated inequalities between children in different positions in the consumption distribution of their countries, but we did not examine inequalities between children with different absolute living standards: the children in the poorest quintile in Brazil may be poor by Brazilian standards but may be relatively well off by, say, the standards in Côte dIvoire.
- We looked solely at inequality and did not try to link inequality with the average mortality rates to get a sense of how countries fared on balance. The low level of inequality in Pakistan is of limited consolation, since the average infant and under-five mortality rates are so high. It should be borne in mind that policy-makers are likely to be willing to trade off inequalities in health against averages.
- Finally, the paper has focused on the measurement of inequalities, not on explaining them. The results suggest that, for the most part, inequalities in infant and under-five mortality favour the better-off, and that these inequalities vary between countries. However, nothing has been said about why inequalities favour the better-off, why they are higher in some countries than in others, and what policies might be most cost-effective in reducing them. These matters deserve special attention in future work.

Acknowledgements
I am grateful for the support of the Visiting Fellow Programme and the Health, Nutrition and Population Sector of the World Bank, and to Jacques van der Gaag and Alex Preker for arranging my visit to the World Bank. My thanks also go to: Ed Bos for his help in calculating mortality rates: Giovanna Prennushi for help with the Nepal data; Diane Steele for her speedy transmission of LSMS data sets and responses to my queries; Dave Gwatkin for helpful conversations; and participants at seminars at the ECuity Project, the Global Health Equity Initiative, the London School of Hygiene and Tropical Medicines Public Health Forum, the World Bank and the World Health Organization for helpful comments.
References
1. Sector strategy: health, nutrition and population. Washington, DC, World Bank, 1997.
2. The world health report 1999: making a difference. Geneva, World Health Organization, 1999.
3. van Doorslaer E et al. Income-related inequalities in health: some international comparisons. Journal of Health Economics, 1997, 16: 93112.
4. Sen A. Mortality as an indicator of economic success and failure. Economic Journal, 1998, 108: 125.
5. Step-by-step guide to estimation of child mortality. New York, United Nations, 1990.
6. Kakwani N, Wagstaff A, van Doorslaer E. Socioeconomic inequalities in health: measurement, computation and statistical inference. Journal of Econometrics, 1997, 77: 87104.
7. Wagstaff A, Paci P, van Doorslaer E. On the measurement of inequalities in health. Social Science and Medicine, 1991, 33: 545557.
8. Pamuk E. Social class inequality in infant mortality in England and Wales from 1921 to 1980. European Journal of Population, 1998, 4: 121.
9. Buhmann B et al. Equivalence scales, well-being, inequality and poverty. Review of Income and Wealth, 1988, 34: 115 142.
10. Hentschel J, Lanjouw P. Constructing an indicator of consumption for the analysis of poverty: principles and illustrations with reference to Ecuador. Washington DC, World Bank, 1996 (Living Standards Measurement Study, Working Paper No. 124).
11. Hill K, Yazbeck A. Trends in child mortality, 196090: estimates for 84 developing countries. Washington, DC, World Bank, 1994 (World Development Report 1993, Background Paper No. 6).
12. Curtis SL. Assessment of the quality of data used for direct estimation of infant and child mortality in DHS-II surveys. Calverton, MD, Macro International Inc, 1995.
13. [National population and health survey 1996.] Calverton, MD, Macro International Inc, 1997 (in Portuguese).
1 Correspondence should be addressed to Dr Wagstaff at the former address.
a The concern that is evident here is with those health inequalities that are systematically associated with economic status. It is of interest but outside the scope of this paper to ask why this specific dimension of health inequality has attracted so much interest among policy-makers and researchers, and why work on overall health inequalities has received far less attention. Both are, of course, inequalities pure inequalities look simply at inter-individual differences in health whilst socioeconomic inequalities look only at those inter-individual differences that are linked to differences in socioeconomic status. The term "inequality" is equally applicable to each type, and in neither case does the use of the term "inequality" of itself carry any connotation that the differences under examination are unjust or inequitable.
b One of the few studies for the industrialized countries was reported by van Doorslaer et al. (3); it examined inequalities in self-assessed health across income groups.
c There is also a shortage of research on the causes of health inequalities, especially empirical research aimed at decomposing inequalities or quantifying the relative impacts of alternative policy options to reduce health inequalities.
d LSMS and the Cebu Longitudinal Health and Nutrition Survey are ongoing data-collection exercises. Further details are available at http://www.worldbank.org/lsms and http://www.cpc.unc.edu/projects/cebu/cebu_home.html, respectively.
e This is not to say that they are free from bias. It seems plausible that the poor may be less inclined to report childhood deaths than the better-off. It also seems plausible that poor women may be comparatively susceptible to the factors giving rise to miscarriage and stillbirth, so that if live births are focused on the whole picture may not be seen.
f The incomplete histories contain, for each woman of fertile age, information on the number of children born alive and on the number of deaths. Estimates of mortality rates can be made only by superimposing these data on model life tables (5). Complete histories record, for each woman of fertile age, the date of birth of each child and the date of death if applicable. These data allow direct estimates of mortality rates to be made. Some LSMS surveys, including the South African survey used in the present paper, fall short of the complete fertility history but contain information on the number of deaths between birth and one year of age and between one and five years of age. It is not clear, however, how this additional information can be used to obtain estimates that are more precise than the indirect ones.
g Several studies are measuring mortality inequalities across groups formed by ranking households by the first principal component in a principal components analysis of a variety of measures of housing and ownership of consumer durables.
h See Kakwani, Wagstaff & van Doorslaer (6) for further details on equation (1) and the equations below.
i The UN (5) suggests that these age bands are likely to be the most reliable and that a reasonable rate of mortality would be an unweighted average of the rates for these age bands. Taking an unweighted average standardizes for differences across countries in the age distribution of women, and this is, of course, desirable.
