THEME PAPERS

Defining and measuring health inequality: an approach based on the distribution of health expectancy

Définir et mesurer les inégalités de santé : approche basée sur la distribution de l’espérance de santé

Definición y medición de las desigualdades en salud: enfoque basado en la distribución de la esperanza de salud

E.E. Gakidou^I,1; C.J.L. Murray^II; J. Frenk^III

^IHealth Policy Analyst, Economics Advisory Service, World Health Organization, 1211 Geneva 27, Switzerland
^IIDirector, Global Programme on Evidence for Health Policy, World Health Organization, Geneva, Switzerland
^IIIExecutive Director, Evidence and Information for Policy, World Health Organization, Geneva, Switzerland

ABSTRACT

This paper proposes an approach to conceptualizing and operationalizing the measurement of health inequality, defined as differences in health across individuals in the population. We propose that health is an intrinsic component of well-being and thus we should be concerned with inequality in health, whether or not it is correlated with inequality in other dimensions of well-being. In the measurement of health inequality, the complete range of fatal and non-fatal health outcomes should be incorporated. This notion is operationalized through the concept of healthy lifespan. Individual health expectancy is preferable, as a measurement, to individual healthy lifespan, since health expectancy excludes those differences in healthy lifespan that are simply due to chance. In other words, the quantity of interest for studying health inequality is the distribution of health expectancy across individuals in the population. The inequality of the distribution of health expectancy can be summarized by measures of individual/mean differences (differences between the individual and the mean of the population) or inter-individual differences. The exact form of the measure to summarize inequality depends on three normative choices. A firmer understanding of people’s views on these normative choices will provide a basis for deliberating on a standard WHO measure of health inequality.

Keywords: analysis of variance; cohort effect; health status indicators; longevity; risk factors; social justice; socioeconomic factors.

RÉSUMÉ

Le présent article propose un cadre qui permet, à partir de quatre notions clés, de conceptualiser la mesure des inégalités de santé et de la rendre opérationnelle.
• Premièrement, il y a le principe selon lequel la santé est un élément intrinsèque du bien-être et par conséquent nous devons nous intéresser aux inégalités de santé, qu’elles soient ou non corrélées avec les inégalités touchant à d’autres aspects du bien-être.
• Deuxièmement, la mesure des inégalités de santé doit refléter la variété des issues, fatales ou non. Cette notion est opérationnalisée grâce au concept de durée de vie en bonne santé.
• Troisièmement, l’espérance de santé individuelle est préférable à la durée de vie en bonne santé individuelle pour rendre compte de la mesure des inégalités de santé car elle exclut les différences de durée de vie vécue en bonne santé simplement dues au hasard. En d’autres termes, le paramètre intéressant dans l’étude des inégalités de santé est la distribution de l’espérance de vie parmi les individus d’une population.
• Quatrièmement, il est possible de résumer l’inégalité de la distribution de l’espérance de santé par la mesure des écarts individuels par rapport à la moyenne (c’est-à-dire les écarts entre les individus et la moyenne pour la population) ou la mesure des écarts inter-individus. La formulation exacte de la mesure résumant les inégalités dépend de trois choix normatifs. Une meilleure compréhension de l’avis des personnes concernant ces choix normatifs servira de base à l’étude d’une mesure normalisée de l’OMS des inégalités de santé.
L’accent mis sur l’inégalité des risques sanitaires en fonction de l’âge (déterminants de la distribution de l’espérance de santé) pourrait renouveler l’intérêt pour certains problèmes de santé, par exemple les nombreuses expositions professionnelles qui n’ont pas une influence considérable sur le niveau moyen de l’espérance de santé de la population mais qui peuvent contribuer aux risques sensiblement élevés menaçant une petite minorité.
Il faudra, pour mesurer la distribution de l’espérance de santé, utiliser les données des enquêtes transversales sur la prévalence de diverses issues non fatales. Lorsqu’on mesure les inégalités de santé, il s’agit essentiellement de comparer la distribution des états de santé des individus au sein des populations, et de comparer entre elles les distributions dans des populations différentes.
Il existe un consensus de plus en plus large selon lequel l’amélioration du niveau moyen de santé n’est pas un indicateur suffisant des qualités d’un système de santé. La manière dont cette amélioration est répartie est un aspect tout aussi important de la qualité. Si nous voulons placer les inégalités de santé au cœur du débat politique, nous devons mettre au point de meilleures méthodes de mesure. Ce sera le seul moyen d’évaluer la véritable ampleur du problème et de suivre les progrès accomplis pour le résoudre.

RESUMEN

En este artículo se propone un marco para conceptualizar y materializar la medición de las desigualdades sanitarias con arreglo a cuatro nociones fundamentales.
• En primer lugar, el principio de que la salud es un componente intrínseco del bienestar y de que, por lo tanto, las desigualdades sanitarias deben ser motivo de preocupación, estén o no relacionadas con otras dimensiones del bienestar.
• Segundo, las mediciones de las desigualdades sanitarias deben reflejar todo el espectro de resultados sanitarios, mortales y no mortales. Esta idea se puede aplicar mediante el concepto de años de vida sana.
• Tercero, a la hora de medir las desigualdades sanitarias, las esperanzas de salud individuales son preferibles a los años de vida sana individuales, ya que las primeras no incluyen las diferencias en los segundos debidas simplemente al azar. En otras palabras, el dato de interés para estudiar las desigualdades sanitarias es la distribución de la esperanza de salud entre los individuos en la población.
•Cuarto, las desigualdades en la distribución de la esperanza de salud pueden resumirse midiendo las diferencias individuales respecto a la media (p. ej., las diferencias entre el individuo y la media de la población) o las diferencias interindividuales. La forma exacta que adopte esa medida sinóptica de las desigualdades dependerá de tres decisiones normativas. Un más profundo conocimiento de las opiniones de las personas acerca de estas decisiones normativas permitirá fundamentar la búsqueda, por parte de la OMS, de una medición estándar de las desigualdades sanitarias.
Centrando la atención en las desigualdades relacionadas con los riesgos para la salud específicos de cada edad (que inciden en la distribución de la esperanza de salud), es posible reavivar el interés en algunos problemas de salud, como por ejemplo muchas exposiciones ocupacionales específicas que no contribuyen sensiblemente a la esperanza de salud media de la población pero pueden contribuir a aumentar considerablemente los riesgos para una pequeña minoría.
Para medir la distribución de la esperanza de salud habrá que emplear datos de encuestas transversales sobre la prevalencia de diversos resultados de salud no mortales. La medición de las desigualdades en salud consiste fundamentalmente en comparar la distribución del estado de salud de los individuos en las poblaciones y en comparar las distribuciones observadas en distintas poblaciones.
Crece el consenso en torno a la idea de que la mejora de los niveles medios de salud no constituye un indicador suficiente del funcionamiento del sistema sanitario. La distribución de esas mejoras constituye una dimensión igualmente importante de ese funcionamiento. A fin de situar las desigualdades sanitarias en el centro del debate de las políticas, debemos desarrollar mejores métodos para medirlas. Sólo así podremos determinar la verdadera magnitud del problema y vigilar los progresos realizados para solucionarlo.

Introduction

Health inequalities are prominent in the policy agenda (1–20). Average achievement is no longer considered a sufficient indicator of a country’s performance on health; rather, the distribution of health in the population is also key. WHO is interested in measuring health inequality as a distinct dimension of the performance of health systems (21). We define health inequality to be variations in health status across individuals in a population (14). This approach, which is consistent with the measurement of inequality in other fields, such as economics, allows us to perform cross-country comparisons and study the determinants of health inequality (22).

This paper addresses the question of measuring health inequalities as distinct from measuring average levels of health. The trade-off between policies that improve the average level of health and those that primarily reduce inequalities in health is an important area of debate. How that trade-off should be resolved is not, however, the subject of this paper.

In the first section, we ask what is the quantity that we would fundamentally want to be equally distributed in a population. In other words, we attempt to answer the classic question in the context of health: equality of what (23)? It is critical for a debate on health inequality first to articulate what the quantity of interest is and why, and then to proceed to measure it, depending on the available data. In the second section, we discuss various ways of summarizing the distribution of the quantity of interest and of calculating an index of health inequality. We also address the three distinct normative issues that are raised. In the third section, we talk about the overall WHO strategy for measurement, and we conclude by highlighting the critical relevance to research and policy formulation that this approach of measuring health inequality will have.

Equality of what?

In addressing the question "What would we like to be equally distributed in the population", several ethical and technical issues arise. Would we consider perfect equality to be when all individuals live the same number of years? When they enjoy the same level of health? When they have exactly the same health status at all points in their lives? In this section we address some of the normative issues surrounding the choice of the quantity that we would like to have equally distributed in a population.

Equality of healthy lifespan

Imagine a cohort of individuals born in the year 2000. What would we need to observe to say that there was complete equality in health among the individuals in this cohort? One starting point might be to argue that everyone in the population should have the same healthy lifespan. In other words, we would like all members of a cohort to live the same number of years and for them to have had on average the same health status during their lives.

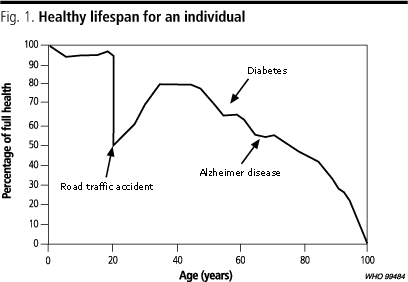
Healthy lifespan is a summary measure of survival and of the non-fatal health outcomes weighted by their preference weights. There is an extensive literature on summary measures of population health that reflect both mortality and non-fatal health outcomes (for an overview, see 24). In the health economics literature, there is an extensive literature on quality-adjusted life years, which are a measure of individual health gain through interventions that incorporates changes in survival and in the quality of health state (see, for example, 25, 26). The notion of a healthy lifespan is essentially the same concept but applied to an individual over the entire lifespan. As an example, Fig. 1 illustrates the healthy lifespan for an individual i. If that same individual had lived for 100 years in full health and then suddenly died, the healthy lifespan would be the whole area of the graph – equal to 100 years. But this individual experienced some decrements from full health, so we represent the healthy lifespan by a different curve, as shown in Fig. 1. The individual shown in Fig. 1 was born in full health, had a motor vehicle accident at 25 years of age, experienced diabetes at 50 years of age and Alzheimer disease at 65 years of age. The area under the curve represents the individual’s healthy lifespan, or in other words, the number of years lived in full health that would be equivalent to the 100 years he or she actually lived with part of the time in states worse than full health. The calculation of healthy lifespan for individual i depends on the weights that are assigned to health states worse than full health; the methods and debates surrounding the measurement of health state weights are addressed elsewhere (27–32).

We need to distinguish between individuals’ healthy lifespans and the set of health risks that they are exposed to at each age of their lives. Health risks are the probabilities of death and of incidence and remission of non-fatal health outcomes that individuals face at each age. We are not able to measure health risks at the individual level, but we are developing methods to approximate them. By combining across all ages an individual’s risks of being in a state less than full health, we can calculate health expectancy, i.e. the expected number of years lived in full health. Health risks can be seen as underlying healthy lifespan or healthy lifespan may be considered the realization of a set of health risks.^a

For all individuals in a cohort to have equal healthy lifespans, two conditions are necessary and sufficient: individuals all have equal health expectancies; and individuals’ risk curves of death, and incidence and remission for non-fatal health outcomes are rectangular. Equal health expectancies mean that the areas under the health survivorship functions (Fig. 2) are equal.^b A rectangular risk curve means that the risks of mortality, incidence, and remission are either zero or one at all ages.^c Because it is essentially impossible for all risk curves to be rectangular, e.g. we will never be able to reduce the risk of injury to zero, the ideal of equal healthy lifespans will never be realized.

In addition, differences in healthy lifespans that are strictly due to chance may not be relevant to measuring health inequality. Individuals faced with exactly the same health survivorship function may have very different healthy lifespans because of chance. Fig. 2a illustrates a particular health survivorship function by age which corresponds to a health expectancy of 56.5 years, and Fig. 2b the distribution of healthy lifespans observed in a population where all individuals were exposed to the distribution of health risks shown in Fig. 2a. At the outset, everyone in this population had a healthy life expectancy of 56.5 years, but due solely to chance, healthy lifespans range from 1 year to 110 years. It is impressive that all of the variation in healthy lifespan seen in Fig. 2b resulted from complete equality in health risks.

For example, at 20 years of age, every individual in the population had a probability of 93% of being in full health; by chance, out of 100 people, about 93 would be in full health at 20 years of age, while the other 7 would not. The risk was the same for all individuals but there was inequality in the outcome. We claim that we are not interested in the inequality that has arisen from chance (or luck) since at the outset all individuals had exactly the same risk. This argument about excluding luck from considerations of equality is well established in the literature on equity. Sen (23), for example, argues that we should want individuals to have equality of capabilities, and not equality in the realization of their capabilities — which he calls functioning.

Equality of healthy lifespan could only be realized if risks of incidence and remission of non-fatal health outcomes, and risks of mortality, were either zero or one for the entire population. Given that this is unfeasible and that it is unlikely that differences in level of health inequality observed across countries are due to different levels of luck or chance in those countries, we are more interested in the distribution of health risks across individuals in a population and comparing these distributions across populations.

Equality of health risks

Each individual has a profile of health risks by age that can be summarized in a health survivorship function (similar to the one shown for a cohort in Fig. 2a). This profile of health risks can be characterized by two distinct attributes. First, the area under the curve shown in Fig. 2a is the health expectancy of the individual: the average healthy lifespan for an individual faced with this health survivorship function.^d Second, the shape of the health survivorship curve may differ while the area under the curve remains constant.

Both differences in health expectancies across individuals and differences in the shape of health risks across age can contribute to unequal healthy lifespans. To help understand the contribution of these two factors to the inequality of healthy lifespans, we will take advantage of the often observed linear relationship between the logarithm of age-specific mortality rates and age (35, 36).^e

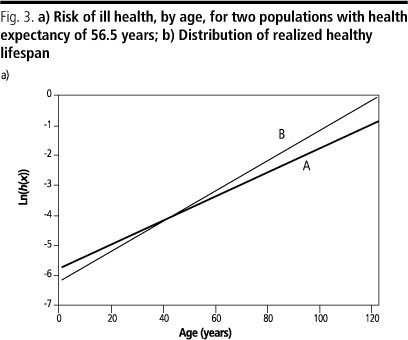
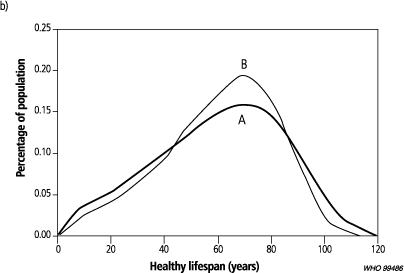
Fig. 3a shows the logarithm of the risk of an ill-health outcome or death for two different populations. In each of the populations all individuals have an identical set of ill-health risks by age, as shown, and health expectancy in each population is 56.5 years. Because the slope of the health risk curve in population A is lower than in population B, the distribution of healthy lifespan (shown in Fig. 3b) for population A has a lower variance than the distribution for population B (variance of 437 for population A versus 568 for B), although they have the same mean.

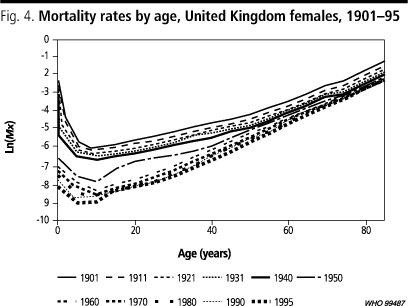
Silber (37) and LeGrand (38, 39) have sought to measure the inequality in the age of death — not healthy lifespan, but the concept is the same, applied solely to risks of death — due to variations in the slope of the logarithm of death rate. Fig. 4 illustrates for women in the United Kingdom a generally observed phenomenon: as mortality declines, the slope of the logarithm of the death rate increases. In other words, there is a strong relationship between the level of mortality and the inequality in the age of death (or years of life lived) that is contributed by the slope of the curve of the logarithm of death rate. Not surprisingly, LeGrand and Silber conclude that as mortality declines inequality measured in this way declines.

If everyone in populations A and B has an identical health expectancy but the age profile of health risks differs only in the slope and intercept of the logarithm of health risks as a function of age, is this contributor to the inequality in healthy lifespan relevant to measuring health inequality? There are a number of arguments that suggest that variation in the average pattern of health risks between populations may not be of much substantive interest. First, there is across populations a strong relationship between the slope of the mortality risk curve and age — and presumably the health risk function and age — such that inequality measured in this way decreases as mortality declines. Second, holding health expectancy constant, there are few policies or interventions to alter the slope of this relationship curve and thus reduce inequality in healthy lifespan. Third, it is not at all clear that everyone would share a common preference for the age profile of health risks.

Studies of social group differences and small area analyses have shown that, within a cohort, there is great variation across individuals in health expectancy (1, 12, 15, 40–42). Some individuals face higher risks of ill health and mortality at every age and others face much lower risks. This variation in health expectancy across individuals at a given age is not reflected in the average health survivorship curve of the population. The health survivorship function shows the average probabilities, without any additional information on how these probabilities are distributed across the population.

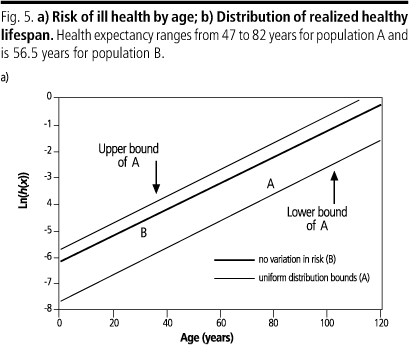
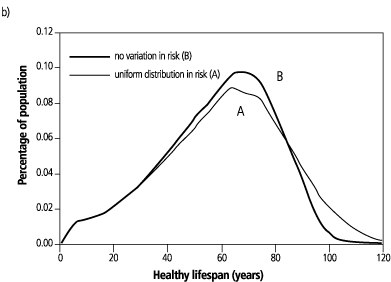
Fig. 5 illustrates the healthy lifespan for a population where individual health expectancies vary from 47 years to 82 years but the slope of the logarithm of health risk function is the same for all individuals. All individuals’ health survivorship functions lie between the bounds shown in Fig. 5a, and are parallel to the bounds. The thicker curve in the middle represents the average risk of ill-health for the population at each age, which corresponds to a health expectancy of 56.5 years. Fig. 5b shows that a population in which the health risk curves lie anywhere between the two bounds shown in Fig. 5a, will have almost the same inequality in terms of healthy lifespans as a population in which all individuals have the same health risk curve (curve B in Fig. 5a). So, in terms of healthy lifespan the two populations have almost the same amount of health inequality; however, looking at the distribution of expected lifespan, or health expectancy (Fig. 5a), most would agree that the population where the health expectancies of individuals lie anywhere in the range 47–82 years has much greater health inequality than the population where health expectancy is 56.5 years for all individuals.

Variation across individuals in health expectancy seems much more important than differences between populations in terms of the slope of the average health risk curve as a function of age.

Fig. 5 also illustrates an important phenomenon in observing any cohort. The average health expectancy is 56.5 years but the realized average cohort lifespan is 58.7 years. The high-risk individuals tend to die at younger ages so the realized mortality at older ages reflects the risks of those with better health expectancies. This selective effect leads to the paradoxical situation that inequality in health expectancy will increase the average realized cohort lifespan.

Fig. 5a also indicates that the chance component in the realization of the expectation is large. The difference between the distributions of health expectancy is very large, ranging from no variation for population B to a large variation for population A, but the difference in the distribution of the outcome (Fig. 5b), i.e. healthy lifespan, is not. A remarkable increase in inequality of health expectancy has a relatively small effect on the distribution of healthy lifespan.

We believe that the distribution of health expectancy for a cohort is of more interest in studying health inequality than the distribution of healthy lifespans. Likewise, we think that the shape of the average health risk curve or variation in the shape of health risk curves holding health expectancy constant may be of interest; however, for the study of health inequality we find it to be less relevant than simply the distribution of health expectancy.

The distribution of health expectancy attributable to unavoidable factors or choice

One might argue that we should be uninterested in two components of the distribution of health expectancy for a cohort: the component that is not amenable to change and the component that arises from fully informed choices of individuals to decrease their health expectancy through the pursuit of risky activities.

If there were differences in health expectancy that could never be remedied either with current or future technology, one could perhaps persuasively argue that we should be uninterested in this, just as we have argued that we are uninterested in the dispersion of healthy lifespans strictly due to chance. But which component of the distribution of health expectancy is not amenable to intervention? That due to genes? That due to chance during birth? In both cases, the argument that we cannot intervene to change the effects on the distribution of health expectancy is most likely specious. With current improvements in technology and future progress, it is likely that these components of the distribution of health expectancy will become amenable to change and thus should not be excluded from a measure of health inequality. Perhaps as important is the argument that there is little evidence of significant cross-population variation in the contribution of genes, etc. The component of health expectancy distribution due to unavoidable factors is likely to be small and completely impossible to assess. From here on, we will assume that it is best to not worry about this aspect.

What about volition? How much of the distribution of health expectancy for a population is due to fully informed choices of individuals who have a taste for risky behaviour? This seems like a very slippery slope. Which choices affecting health are fully informed? Would we exclude the effects of tobacco on health expectancy — which are likely to be very great — because smoking is a choice? Even if we claim that the choice was informed, should it be excluded? We would argue that it should not be excluded. First, in most cases, health risks are not taken because of a love of risky behaviour, but rather for other less informed reasons.^f Second, the true volitional component of the distribution of health expectancy is likely to be very small and can well be ignored. This argument is similar to ones in the field of income inequality, where the variation in the distribution of income due to different leisure–income trade-offs in the population is routinely ignored in the measurement of income inequality.

From cohort to period measures of health expectancy

If we could directly measure every individual’s risks of incidence, remission and mortality at each age, we would be able to construct the distribution of health expectancies for a cohort. From a policy perspective, waiting over 100 years to measure health inequality for each birth cohort would not be useful. Since health inequality is a critical component of health system performance, we need to measure it using only information collected over one period of time. In other words, we need to conceptualize a period measure of the distribution of health expectancy.

In the estimation of a period measure we only have information on individual, i, at one age, a. To estimate the distribution of health expectancies, we need to relate this measurement to the distribution of risks at another age for a different set of individuals. We need a formal principle for linking observed risks in different individuals in order to estimate the health expectancy of a hypothetical birth cohort, exposed to currently observed risks. To estimate the period distribution of health expectancy, we could follow one of two strategies. A variable, such as a socioeconomic status indicator, could be used to link individuals at different ages. This approach would underestimate the distribution of health expectancies because it assumes that all variation in health risks is predicted by the socioeconomic variable selected. Alternatively, we could assume an arbitrary correlation of risk between age groups, less than or equal to one. It is a basic challenge to estimate risk distributions, since they are largely unobservable.

In summary, we argue that the most relevant quantity of interest for studying health inequality is the distribution of health expectancy across individuals, constructed for a period, using a clearly defined method for linking the distributions of health risks at different ages.

Summarizing the distribution of health expectancy in a measure of health inequality

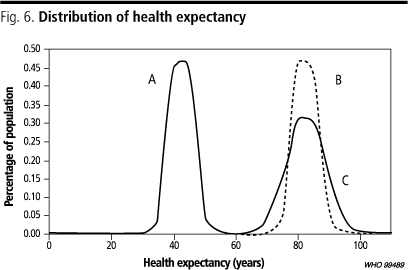
Fig. 6 illustrates the distribution of health expectancies for three populations, A, B and C. Which distribution represents a more unequal distribution of health expectancy? If the x-axis in the graph were income, rather than health expectancy, most people would agree that distribution B is less unequal than C and A. This simple conclusion is based on the concept of decreasing marginal utility of income, namely that an extra dollar generates less utility as income rises. Distribution B has the same variance as A, but a higher mean. In terms of a commonly used measure of inequality, the Gini coefficient, distributions A and C have the same amount of inequality, while distribution B has lower inequality than A and C. While some people may be in agreement that distributions A and C have equal amounts of inequality with regard to income, this finding may be met with less agreement in the context of health. The notion of declining marginal utility does not apply as persuasively. Some would say that C is clearly worse than A or B and that they cannot distinguish between A and B. The vast literature on measuring income inequality (23, 45–48) is very helpful in the design of a health inequality measure, but this simple example illustrates that health has some fundamental differences from income that require special consideration. To date, in the literature on measuring health inequality, there has been little substantive discussion on summary measures of distributions of health.

Two families of health inequality measures

Based on the wide array of measures used to summarize the distribution of income (48) and taking into account the fact that absolute, and not just relative, differences in health expectancies may matter, we propose two families of measures: individual/ mean differences and inter-individual differences.

Individual/mean differences. Measures of individual/mean differences compare each individual’s health to the mean of the population. The general form is:

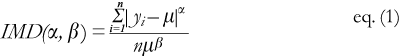
where y_i is the health of individual i, m is the mean health of the population, and n is the number of individuals in the population. The parameter a changes the significance attached to differences in health observed at the ends of the distribution, compared to those observed near the mean of the distribution. The parameter b controls the extent to which the measure is purely relative to the mean or absolute. Common examples of individual/mean differences are the variance when a = 2 and b = 0, and the coefficient of variation when a = 2 and b =1. However, many other individual/mean difference measures are possible. When b =1 the measure is strictly relative, and when b = 0 it is measuring absolute deviations from the mean; but b could be any value between zero and one reflecting some mix of concern between relative and absolute individual/mean difference.

Inter-individual differences. Another family of measures is based on comparing each individual’s health to every other individual’s health, rather than comparing each individual to the mean of the population. We propose the general form of these measures to be:

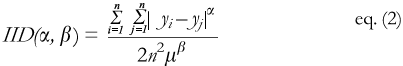
where y_i is the health of individual i and y_j is the health of individual j, m is the mean health of the population, and n is the number of individuals in the population. The parameters a and b are the same as for the individual/mean measures described above. A well-known example of this family is the Gini coefficient (49) often used to measure income distribution, where a = 1 and b = 1. The Gini coefficient is often represented as being derived graphically from the Lorenz curve (50) of a population, but in fact is algebraically equal to eq. (2) above. It is worth noting that when a = 2 the individual/mean difference and the inter-individual difference for any given population distribution are identical. For any other values of a they are different.

Choosing a single index of health inequality

For standard comparisons we need to choose a single index of health inequality to summarize the distribution of health expectancy for a population. This choice requires the resolution of three fundamentally normative issues: which family of measures should be used; what should be the value of a; and what should be the value of b. Individual preferences for these normative choices can be elicited through a series of questions that isolate the effect of each on the index of inequality.

We provide illustrative examples of what these choices entail. For reasons of simplicity, we use a population of seven individuals. In each example we transfer years of health expectancy from an individual who is better-off (i.e. higher health expectancy) to an individual who is worse-off. The transfers will be described in the text and are also depicted in Fig. 7–9. There are three types of choices to be made. For each choice we present two populations and the question is "Which represents a greater decrease in inequality: the transfer in population A or the transfer in population B"?

Relative versus absolute inequality. One of the key choices is whether we are more concerned about absolute differences in health, relative differences in health, or a mix of both. With this question we attempt to measure the extent to which individuals are concerned about relative inequality, absolute inequality or some mixture. The situation depicted in Fig. 7 is the following: populations A and B have similar distributions of life expectancy across the seven individuals, but at different levels. In population A the mean is 20 years, while in population B the mean is 60 years. In population A, 5 years of life expectancy are transferred from an individual whose life expectancy is 35 years to an individual whose life expectancy is 5 years. In population B, 5 years of health expectancy are transferred from an individual with health expectancy of 75 years (highest in the population) to an individual with health expectancy of 45 years (lowest in the population). Which of the two transfers results in a greater decrease of health inequality?

With questions such as this, we can elicit people’s preferences for a value of b, between zero and one.

Intensity of health gain/loss. The second normative choice has to do with whether gains or losses of health that occur at the ends of the distribution should be treated differently from those that occur near the mean. Consider the two reductions in health inequality depicted in Fig. 8. Both populations are at the same level of health expectancy, with a mean value of 20 years. In population A, 5 years of health expectancy are transferred from the individual with the highest value (35 years) to the individual with the lowest value (5 years). In population B, 5 years of health expectancy are transferred from the individual with health expectancy of 30 years to the individual with a health expectancy of 10 years. Which of the two transfers represents a greater decrease in health inequality?

If population A is chosen, the measure used would need to give more weight to transfers of health occurring at the ends of the distribution. If the respondent is indifferent, all transfers of the same amount should be weighted equally, regardless of where they occur in the distribution. If the choice is population A, a will be greater than 1; if the respondent is indifferent as to which of the two scenarios is chosen, a = 1. By constructing other questions where the amount of health expectancy that is transferred is different in magnitude, the exact value of a could be elicited.

Inter-individual versus individual/mean differences. The third choice refers to the family of measures: individual/mean or inter-individual comparisons. In Fig. 9, the two reductions in health inequality illustrate the choice. Both populations have the same mean value of health expectancy and exactly the same amount of health is transferred in both cases. The initial distribution of health is different in the two populations. In both populations, 15 years of health expectancy are transferred from the individual in the upper end of the distribution (35 years) to the individual at the lower end of the distribution (5 years). The question again is "which of the two scenarios represents a greater decrease in inequality?" Those who prefer A or B are expressing a view that what counts is not only where the individual starts and ends up, but also where the rest of the population is. Those who are indifferent between A and B believe that what is really important is the absolute change achieved, regardless of where other people are in the distribution. In the first case, we would use a measure of inter-individual comparisons, while in the second case we would use a measure of individual/mean differences.

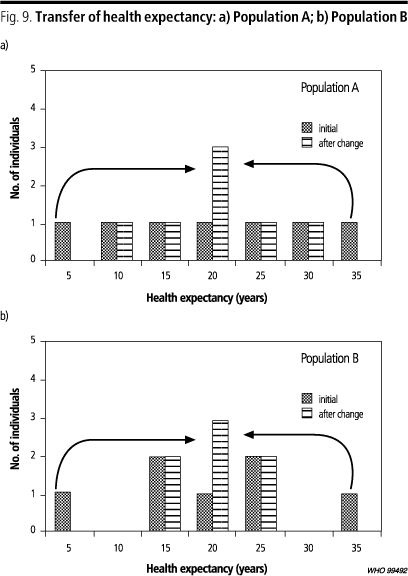
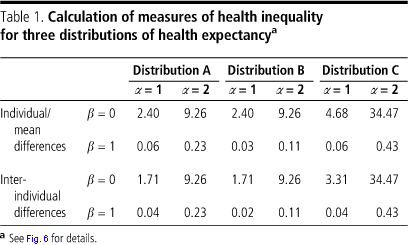
The normative choices about the intensity of the transfer and about the family of measures are not completely separable. Inter-individual comparison measures, even when a = 1, are more sensitive to equivalent transfers of risk farther from the mean. Table 1 shows the inequality for the three distributions in Fig. 6, calculated for a few parameter values of the measures described above.

Through a series of questions, we could elicit individuals’ values for the design of a summary index for the distribution of health expectancy. Population surveys or convenience samples could provide information from a wide range of individuals. We do not propose empirical ethics as a blind tool for resolution of normative choices; rather we believe that the results of measuring these values for a broad range of individuals will be a useful input to a deliberative process for choosing an index of health inequality.

Based on a limited initial investigation, we suspect that most persons will prefer a measure with a mix of absolute and relative inequality, with a bigger weight for differences farther from the mean, and with a consideration of intervening individuals. Yet, these questions clearly require broader empirical assessment of the values held by different persons.

Operationalizing the measurement of inequality in health expectancy

While we have argued that the quantity of interest for measuring health inequality is the distribution of period health expectancy, how can this be measured? Risk is not observed, only outcomes. We believe that the distribution of health risks can be reasonably approximated through a variety of techniques. The combination of these techniques provides a reasonable strategy to estimate the distribution of health expectancy. The strategy can be divided into four distinct approaches: measuring the distribution of child mortality risk; measuring the distribution of adult mortality risk; measuring the distribution of life expectancy and health expectancy through small area analyses; and measuring the distribution of non-fatal health outcomes.

Child mortality risk

We can observe the variation in the proportion of a mother’s children who have died. This provides information at a very fine level of aggregation (namely households) on the distribution of child death risk. Using simulation, we can evaluate the difference in the distribution of outcomes from that which would be expected based on a distribution of equal risk. Data on children ever born and children surviving for women of different ages are widely available from the Living Standards Measurement Studies (LSMS) (51), the Demographic and Health Surveys (DHS) (52) and many censuses and surveys. We have implemented this strategy for measuring child mortality (22).

Adult mortality risk

We do not have good data to measure the distribution of adult mortality. Information on the survivorship of siblings could in principle be used but it would refer to average mortality experience over decades, and the technical challenges have yet to be solved. Other strategies need to be developed.

Distribution of life expectancy or health expectancy for groups

We can divide the population into groups that are expected to have similar health expectancies and measure directly the health expectation for those groups. Inevitably, this will underestimate the distribution of health expectancy. The more refined the groupings, the more we will approximate the true underlying distribution. Small area analyses hold out the promise of being one of the most refined methods for revealing the underlying distribution of health expectancy in a population. For example, a detailed age–sex–race group analysis of counties in the USA has revealed a range in life expectancy of 41.3 years across counties (15).

The distribution of non-fatal health outcomes

Measurement of non-fatal health outcomes on continuous or polychotomous categorical scales provides more information from which to estimate the distribution of risk across individuals. Numerous surveys provide information on self-reported health status, using a variety of instruments. The main problem to date with this information is the comparability of the responses across different cultures, levels of educational attainment and incomes. For example, the rich often report worse non-fatal health outcomes than the poor (53, 54). Problems of comparability must be resolved before such data sets can be used to contribute to estimation of health expectancy in the population.

For WHO, the way forward will be simultaneously to pursue the development of methods and data sets to measure these different dimensions of the distribution of health expectancy. We recognize that there is a great need for new methods to integrate these different measurements into one estimation of the distribution of health expectancy in populations.

Conclusions

In this paper we propose a framework for the measurement of health inequality, which is based on four key notions. First, we start with the principle that health is an intrinsic component of well-being and thus we should be concerned with inequality in health, whether or not it is correlated with inequality in other dimensions of well-being. Second, we propose that any measure of health inequality should reflect the complete range of fatal and non-fatal health outcomes in order to capture the rich complexity of health. We operationalize this notion through the concept of healthy lifespan. Third, we propose health expectancy as an improved measure compared to healthy lifespan, since it excludes those differences in healthy lifespan that are simply due to chance. In other words, the quantity of interest for studying health inequality is the distribution of health expectancy across individuals in the population. Fourth, the inequality of the distribution of health expectancy can be summarized by measures of individual/mean differences or inter-individual differences. The exact form of the measure to summarize inequality depends on three normative choices. A firmer understanding of people’s views with regard to these normative choices will provide a basis for discussion of a standard WHO measure of health inequality.

Our approach contrasts with that proposed by LeGrand (38, 39) and Silber (37), whose primary concern is with the shape of the average population mortality rate as a function of age. Their approach indicates that health inequality is decreasing worldwide, but their conclusions are entirely attributable to the fact that the shape of the curve of average mortality risks across ages changes in a predictable fashion as life expectancy increases. We argue that we should focus on the distribution of health expectancy across individuals. There is no reason to expect that this distribution steadily narrows as average health expectancy increases. Early results on the distribution of child death risks across countries indicate that there is no relationship between the level of child death and the distribution of risk across individuals (22).

A focus on the inequality of age-specific health risks may reinvigorate interest in some health problems. For example, many specific occupational exposures are not major contributors to average levels of population health expectancy but may contribute to markedly elevated risks for a small minority. As we better quantify the distribution of health expectancy, the role of occupational and local environmental exposures in contributing to risk inequality may become apparent. Interest in inequality in health risks in developed countries may also draw attention to the impressive inequality in adult male mortality risk. In the USA, there is considerably more inequality in adult male mortality risk than in child or adult female mortality risks (15).

Measuring the distribution of health expectancy will involve cross-sectional survey data on the prevalence of non-fatal health outcomes. Measuring health inequality is fundamentally about comparing the distribution of the health status of individuals within populations and comparing distributions of different populations. If self-reported responses from the application of various health status surveys (using instruments such as SF-36, EUROQOL, or activities of daily living) are to be used in estimating health expectancy, special attention will need to be paid to the comparability of these responses across cultural groups. There is evidence that current instruments for measuring health status in surveys may not be comparable (54–56). It is hoped that the work on inequality will improve the comparability of health status survey responses across cultural groups.

There is growing consensus that improvement in average levels of health is not a sufficient indicator of health system performance. The distribution of such improvement is an equally important dimension of performance. In order to place health inequality at the centre of the policy debate, we must develop better ways of measuring it. That will be the only way of ascertaining the true magnitude of the problem and of monitoring progress towards its solution.

Acknowledgements

We are indebted to the following individuals for useful input and comments: Gary King, Rafael Lozano, Joshua Salomon, Daniel Wikler, Sarah Marchand and Philip Musgrove.

References

1. Acheson D. Independent inquiry into inequalities in health. London, The Stationery Office, 1998.         

2. Antonovsky A. Social class, life expectancy and overall mortality. Milbank Memorial Fund Quarterly, 1967, 45 (2): 31– 73.         

3. Barker J. Inequalities — whose health for all? Health Visit, 1990, 63 (7): 232–233.         

4. Beaglehole R, Bonita R. Public health at the crossroads: which way forward? Lancet, 1998, 351: 590–592.         

5. Kaplan G, Lynch J. Whither studies on the socioeconomic foundations of population health? American Journal of Public Health, 1997, 87: 1409–1411.         

6. Judge K et al. Income inequality and population health. Social Science and Medicine, 1998, 46: 567–579.         

7. Kawachi I, Kennedy BP. Income inequality and health: pathways and mechanisms. Health Services and Research, 1999, 34: 215–227.         

8. Krieger N, Fee E. Measuring social inequalities in health in the United States: a historical review, 1900–1950. International Journal of Health Services, 1996, 26 (3): 391–418.         

9. Kunst AE et al. International variation in socioeconomic inequalities in self reported health. Journal of Epidemiology and Community Health, 1995, 49 (2): 117–123.         

10. Mackenbach JP. Socioeconomic inequalities in health in The Netherlands: impact of a five year research programme. British Medical Journal, 1994, 309: 1487–1491.         

11. Mackenbach JP, Gunning-Schepers LJ. How should interventions to reduce inequalities in health be evaluated? Journal of Epidemiology and Community Health, 1997, 51: 359–364.         

12. Marmot MG et al. Health inequalities among British civil servants: the Whitehall II study. Lancet, 1991, 337: 1387– 1393.         

13. Marmot M et al. Social inequalities in health: next questions and converging evidence. Social Science and Medicine, 1997, 44 (6): 901–910.         

14. Murray CJL et al. Health inequalities and social group differences: what should we measure? Bulletin of the World Health Organization, 1999, 77: 537–543.         

15. Murray CJL et al. U.S. patterns of mortality by county and race: 1965–1994. Cambridge, MA, Harvard School of Public Health and National Center for Disease Prevention and Health Promotion, 1998.         

16. Power C, Matthews S. Origins of health inequalities in a national population sample. Lancet, 1997, 350: 1584–1589.         

17. Townsend P. Widening inequalities of health in Britain: a rejoinder to Rudolph Klein. International Journal of Health Services, 1990, 20: 363–372.         

18. Wagstaff A et al. On the measurement of inequalities in health. Social Science and Medicine, 1991, 33: 545–557.         

19. van Doorslaer E et al. Income-related inequalities in health: some international comparisons. Journal of Health Economics, 1997, 16: 93–112.         

20. Whitehead M et al. Setting targets to address inequalities in health. Lancet, 1998, 351: 1279–1282.         

21. Murray CJL, Frenk J. WHO’s framework for assessing health system performance. Geneva, World Health Organization, 1999 (unpublished document, GPE Working Paper Series No.7).         

22. Murray CJL et al. Measuring health inequality: challenges and new directions. In: Leon D, Walt, G, eds. Poverty, inequality and health. London, Oxford University Press, 1999 (in press).         

23. Sen A. Inequality reexamined. Cambridge, MA, Harvard University Press, 1992.         

24. Murray CJL et al. A critical examination of summary measures of population health. Geneva, World Health Organization, 1999 (unpublished document, GPE Working Paper Series No.2).         

25. Fanshel S, Bush JW. A health-status index and its application to health services outcomes. Operations Research, 1970, 18: 1021–1066.         

26. Weinstein MC, Stason WB. Foundations of cost-effectiveness analysis for health and medical practices. New England Journal of Medicine, 1977, 296: 716–721.         

27. Richardson J. Cost utility analysis: what should we measure? Social Science and Medicine, 1994, 39: 7–21.         

28. Torrance GW. Measurement of health-state utilities for economics apprasial: a review. Journal of Health Economics, 1976, 5: 1–30.         

29. Nord E. Methods for quality adjustment of life years. Social Science and Medicine, 1992, 34: 559–569.         

30. Nord E et al. Social evaluation of health care versus personal evaluation of health states. Evidence on the validity of four health-state scaling instruments using Norwegian and Australian Surveys. International Journal of Technology Assessment in Health Care, 1993, 9: 463–478.         

31. Murray CJL. Rethinking DALYs. In: Murray CJL, Lopez, AD, eds. The global burden of disease: a comprehensive assessment of mortality and disability from diseases, injuries, and risk factors in 1990 and projected to 2020. Cambridge, MA, Harvard School of Public Health on behalf of the World Health Organization and the World Bank, 1996.         

32. Ware JE. Standards for validating health measures: definition and content. Journal of Chronic Diseases, 1987, 40: 473–480.         

33. Sanders BS. Measuring community health levels. American Journal of Public Health, 1964, 54: 1063–1070.         

34. Sullivan DF. A single index of mortality and morbidity. HSMHA Health Reports, 1971, 86: 347–354.         

35. Gompertz B. On the nature of the function expressive of the law of human mortality and on a new mode of determining life contingencies. Philosophical Transactions of the Royal Society of London, 1825, 115: 513–585.         

36. Olshansky SJ, Carnes BA. Ever since Gompertz. Demography, 1997, 34: 1–15.         

37. Silber J. Health and inequality. Some applications of uncertainty theory. Social Science and Medicine, 1982, 16: 1663– 1666.         

38. LeGrand J. An international comparison of measures of distributions of ages-at-death. In: Fox J, ed. Health inequalities in European countries. Aldershot, Gower, 1988.         

39. LeGrand J. Inequalities in health and health care: a research agenda. In: Wilkinson RG, ed. Class and health: research and longitudinal data. London, Tavistock Publications, 1986.         

40. Corchia C et al. Social and geographical inequalities in prenatal care in Italy. Prenatal Diagnosis, 1995, 15: 535–540.         

41. Hart CL et al. Inequalities in mortality by social class measured at 3 stages of the lifecourse. American Journal of Public Health, 1998, 88: 471–474.         

42. Hollingsworth JR. Inequality in levels of health in England and Wales, 1891–1971. Journal of Health and Social Behavior, 1981, 22: 268–283.         

43. Parfit D. Reasons and persons. Oxford, Oxford University Press, 1984.         

44. Pigou AC. The economics of welfare. London, Macmillan, 1932.         

45. Kakwani NC. On the estimation of income inequality measures from grouped observations. The Review of Econometrics Studies, 1976, 43: 483–492.         

46. Nygard F, Sandstrom A. Income inequality measures based on sample surveys. Journal of Econometrics, 1989, 42: 81–95.         

47. Dagum C, Zenga M, eds. Income and wealth distribution, inequality and poverty. In: Proceedings of the Second International Conference on Income Distribution by Size: Generation, Distribution, Measurement and Applications, University of Pavia, Italy, 23–30 September, 1989. New York, Springer, 1990.         

48. Sen A. On economic inequality. Oxford, Oxford University Press, 1997.         

49. Gini C. Variabilità e mutabilità. Bologna, Tipogr. di P. Cuppini, 1912 (in Italian).         

50. Lorenz MO. Methods for measuring the concentration of wealth. Journal of the American Statistical Association, 1905, vol.9.         

51. Grosh M, Glewwe P. A guide to living standards surveys and their data sets. Washington, DC, The World Bank, 1995 (updated on 1 March 1996).         

52. Demographic and Health Survey. Internet communication at: http://www.macroint.com/dhs/indicatr/datasearch.asp        

53. Australian Institute of Health and Welfare. Australia’s health: the fifth biennial report of the Australian Institute of Health and Welfare. Canberra, Australian Government Publishing System, 1996.         

54. Murray CJL, Chen LC. Understanding morbidity change. Population and Development Review, 1992, 18: 481–503.         

55. Johansson SR. Measuring the cultural inflation of morbidity during the decline of mortality. Health Transition Review, 1992, 2: 78–89.         

56. Johansson SR. The health transition: the cultural inflation of morbidity during the decline of mortality. Health Transition Review, 1991, 2: 39–68.         

1 Correspondence should be addressed to this author.
a There is a well-established literature on health expectancy as a measure of population health that integrates information on mortality and non-fatal health outcomes (33, 34). We are applying the concept to an individual to summarize ex ante health risks as a function of age.
b For an individual the health survivorship function is:

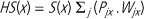
where HS(x) is the health survival at age x, S(x) is the probability of being alive at age x, P_jx is the probability of being in state j at age x (which takes into account both incidence and remission for condition j) and W_jx is the severity weight attached to state j at age x, measured on a scale where zero is equivalent to death and one is full health. If we assume that HS(x) monotonically declines with age, we can summarize the combination of health risks and the severity weight for different health states and mortality into one measure of health risk, h(x), which can be thought of as the sole hazard to which an individual would be exposed such that health survivorship would be HS(x).
c For mortality, rectangular risk curves mean that all individuals have a zero risk of death until some age x, at which the risk becomes 1 for the entire population. For non-fatal health outcomes, rectangular risk curves mean that, at a given age, the risk of incidence of a condition or remission from that condition is either 0 or 1 for the entire population. Individuals’ risk curves may differ as long as health expectancy is the same.
d Formally:

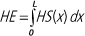
where HE is health expectancy, HS(x) is the probability of being in full health at age x, and L is the limit of human life.
e Gompertz’ Law of Mortality (35) applies only to mortality rates above age 20. Risks of death from birth to age 20 decline with age. Recently, careful analyses of mortality rates over age 75 or 80 have shown that they do not increase as fast as the Law of Mortality would predict (36).
f The cost of being fully informed about the health consequences of different choices is often prohibitively high. Most individuals are forced to make choices with incomplete or incorrect information. When the choice to take a risk and the outcome are separated in time, the rate at which individuals discount the future can profoundly influence choices about health. We would argue, for example, that health inequalities resulting from individuals with high discount rates should be included in measuring health inequality. Some philosophers (43) and economists (44) have long argued that discounting or myopia is a defect of human judgement and can be self-defeating.