ABSTRACT

Objective.

To evaluate, using semiparametric methodologies of survival analysis, the relationship between covariates and time to death of patients with breast cancer, as well as the determination discriminatory power in the conditional inference tree of patients who had cancer.

Methods.

A retrospective cohort study was conducted using data collected from medical records of women who had breast cancer and underwent treatment between 2005 and 2015 at the Hospital da Fundação de Assistencial da Paraíba in Campina Grande, State of Paraiba, Brazil. Survival curves were estimated using the Kaplan–Meier method, Cox regression, and conditional decision tree.

Results.

Women with triple-negative molecular subtypes had a shorter survival time compared to women with positive hormone receptors. The addition of hormone therapy reduced the risk of a patient dying by 5.5%, and the risk of a HER2-positive patient dying was 34.5% lower compared to those who were negative for this gene. Patients undergoing hormone therapy had a median survival time of 4 753 days.

Conclusions.

This paper shows a favorable scenario for the use of immunotherapy for patients with HER2 overexpression. Further studies could assess the effectiveness of immunotherapy in patients with other conditions, to favor the prognosis and better quality of life for the patient.

Keywords
Survival analysis; breast neoplasms; mortality; Brazil

RESUMEN

Objetivo.

Evaluar, mediante métodos semiparamétricos del análisis de supervivencia, la relación entre las covariables y el tiempo hasta la muerte de las pacientes con cáncer de mama, así como la determinación del poder discriminatorio en el árbol de inferencia condicional de las pacientes con cáncer.

Métodos.

Se llevó a cabo un estudio retrospectivo de cohortes con datos recogidos de los expedientes médicos de mujeres con cáncer de mama que recibieron tratamiento entre los años 2005 y 2015 en el Hospital da Fundação de Assistencial da Paraíba en Campina Grande, en el estado de Paraíba (Brasil). Se calcularon las curvas de supervivencia mediante el método Kaplan–Meier, el modelo de regresión de Cox y un árbol de decisiones condicionales.

Resultados.

Las mujeres con subtipos moleculares triple negativos tuvieron un período de supervivencia más corto en comparación con las mujeres con receptores hormonales positivos. La adición del tratamiento hormonal redujo en 5,5 % el riesgo de muerte de la paciente y en un 34,5% el riesgo de muerte de pacientes con cáncer HER2-positivo en comparación con las pacientes negativas para este gen. Las pacientes en tratamiento hormonal tuvieron un tiempo medio de supervivencia de 4 753 días.

Conclusiones.

Este estudio muestra un escenario favorable para el uso de la inmunoterapia en las pacientes con sobreexpresión del HER2. En futuros estudios se podría evaluar la eficacia de la inmunoterapia en pacientes con otras enfermedades, con el fin de favorecer el pronóstico y mejorar la calidad de vida de la paciente.

Palabras clave
Análisis de supervivencia; neoplasias de la mama; mortalidad; Brasil

RESUMO

Objetivo.

Avaliar, por meio de métodos semiparamétricos de análise de sobrevida, a relação entre covariáveis e tempo até a morte em pacientes com câncer de mama e determinar o poder discriminatório na árvore de inferência condicional em pacientes que tiveram câncer.

Métodos.

Estudo de coorte retrospectivo realizado a partir de dados coletados de prontuários médicos de mulheres com câncer de mama, tratadas entre 2005 e 2015 no Hospital da Fundação Assistencial da Paraíba em Campina Grande, no estado da Paraíba, Brasil. As curvas de sobrevida foram estimadas pelo método de Kaplan-Meier, regressão de Cox e árvore de decisão condicional.

Resultados.

As pacientes com subtipos moleculares de tumor triplo-negativo tiveram uma sobrevida menor em comparação com as que apresentavam tumor com receptores hormonais. O acréscimo de hormonioterapia reduziu o risco de morte em 5,5%. O risco de morte foi 34,5% menor em pacientes com HER2+ quando comparadas às que tinham tumores sem a expressão desse gene. A mediana de sobrevida das pacientes tratadas com hormonioterapia foi de 4 753 dias.

Conclusões.

A presente análise revela um cenário favorável para o uso de imunoterapia em pacientes com superexpressão de HER2. Outros estudos devem ser realizados para avaliar a eficácia da imunoterapia em outras doenças e os fatores que favorecem o prognóstico e melhoram a qualidade de vida dessas pessoas.

Palavras-chave
Análise de sobrevida; neoplasias da mama; mortalidade; Brasil

Breast cancer is considered one of the main factors influencing mortality in the female population worldwide (¹1. World Health Organization. Cancer. Geneva: WHO; 2021. Available from: http://www.who.int/cancer/en/. Cited 2021 Jun 19.
http://www.who.int/cancer/en/... ). Studies show an increased incidence of breast cancer in developing countries, due, among other factors, to adoption of an unhealthy lifestyle and increased life expectancy (²2. Torre LA, Siegel RL, Ward EM, Jemal A. Global Cancer Incidence and Mortality Rates and Trends - An Update. Cancer Epidemiol Biomarkers Prev. 2016;25:16–27. https://doi.org/10.1158/1055-9965.EPI-15-0578
https://doi.org/10.1158/1055-9965.EPI-15... ).

From 2020 to 2022, the most prominent cancer institute in Brazil, the National Cancer Institute (Instituto Nacional de Câncer—INCA) estimated an occurrence of 625 000 new cases of breast cancer nationwide (³3. Instituto Nacional de Câncer José Alencar Gomes da Silva, Coordenação de Prevenção e Vigilância. Estimativa 2020: incidência de câncer no Brasil. Rio de Janeiro: INCA; 2019.). In this regard, the Northeast region presented a considerable increase in the incidence rate, from approximately 27 new cases per 100 000 women in 2005 to approximately 64 per 100 000 in 2018 (⁴4. Instituto Nacional de Câncer. Estimativa 2005: incidência de câncer no Brasil. Rio de Janeiro: INCA; 2005., ⁵5. Instituto Nacional de Câncer. Estimativa 2018: incidência de câncer no Brasil. Rio de Janeiro: INCA; 2018.).

Historically, it is known that the mortality rate due to breast cancer is higher in less-developed regions (⁶6. Momenimovahed Z, Salehiniya H. Epidemiological characteristics of and risk factors for breast cancer in the word. Breast Cancer. 2019;11:151–64.). According to the Atlas of Mortality from Breast Cancer, prepared by INCA, while in 2005 the State of Paraiba had 156 deaths from malignant breast cancer, in 2015 this number had risen by almost 60%, reaching 248 (⁷7. Instituto Nacional de Câncer. Atlas da Mortalidade por Câncer de Mama. Rio de Janeiro: INCA; 2020. Available from: https://www.inca.gov.br/aplicativos/atlas-de-mortalidade-por-cancer Cited 2021 Jun 19.
https://www.inca.gov.br/aplicativos/atla... ).

Regarding data analysis on breast cancer, several models have been frequently proposed as alternatives to explain relationships among the variables. The use of survival analysis models aims to describe the probability of survival of individuals under specific conditions (type of treatment, age) after the breast cancer diagnosis. Survival analysis is an area of statistics that aims to analyze the time until the occurrence of a particular event of interest, which is defined as failure or outcome (⁸8. Emmert-Streib F, Dehmer M. Introduction to survival analysis in practice. Mach Learn Knowl Extr. 2019;1(3):1013–38.). A peculiarity is the possibility of censoring presence, which is the partial observation of the response of interest when the individual does not suffer the event during the study period. It is precisely in the censored observations that survival analysis differs from other analyses, such as logistic regression (⁹9. Efron B. Logistic regression, survival analysis, and the Kaplan-Meier curve. J Am Stat Assoc. 1988;83(402):414–25. https://doi.org/10.2307/2288857
https://doi.org/10.2307/2288857... , ¹⁰10. Staley JR, Jones E, Kaptoge S, Butterworth AS, Sweeting MJ, Wood AM, et al. A comparison of Cox and logistic regression for use in genome-wide association studies of cohort and case-cohort design. Eur J Hum Genet. 2017;25(7):854–62. https://doi.org/10.1038/ejhg.2017.78
https://doi.org/10.1038/ejhg.2017.78... ).

Concerning the adjustment of survival models, it is known that the use of covariables affects the lifespan of individuals, giving rise to the need to use regression analysis as a way to include this additional information (¹¹11. Schober P, Vetter TR. Survival analysis and interpretation of time-to-event data: the tortoise and the hare. Anesth Analg. 2018;127(3):792. https://doi.org/10.1213/ANE.0000000000003653
https://doi.org/10.1213/ANE.000000000000... ). In survival analysis, it is possible to collect variables that represent the existing variability in the population, such as age and sex, among others, for use in regressive models. In these cases, two approaches can be initially adopted: parametric models and semiparametric models (¹²12. Colosimo E, Giolo S. Análise de sobrevivência aplicada. 1 ed. São Paulo: Editora Edgard Blucher; 2006.–¹⁴14. Collett D. Modelling Survival Data in Medical Research. Boca Raton, FL: CRC Press; 2015.).

Recursive partitioning for a continuous response, censored, ordered, nominal, and multivariate variables in a conditional inference structure are available in the R party package and partykit (¹⁵15. Hothorn T, Zeileis A. partykit: A modular toolkit for recursive partytioning in R. J Mach Learn Res. 2015;16(118):3905–9. Available from: https://jmlr.org/papers/v16/hothorn15a.html
https://jmlr.org/papers/v16/hothorn15a.h... ), which is free of charge and available from https://cran.r-project.org. The methodology in the party package uses conditional inference as a binary and recursive partitioning method in subsets, and partykit consists of its improved implementation, providing the same approach based on new infrastructure (¹⁶16. Braga LCC, Drummond IN. Extração de informação em bases de dados abertas governamentais através de uma abordagem de mineração descritiva empregando a ferramenta R. Rev Informática Aplicada. 2018;14(1). https://doi.org/10.13037/ria.vol14n1.201
https://doi.org/10.13037/ria.vol14n1.201... ). Predictions can be calculated using the partykit package, which returns predicted means, predicted classes, or predicted mean survival times, and more information about the conditional distribution of the response variable, that is, predicted class probabilities or Kaplan–Meier curves, being a viable alternative to Cox modeling (¹⁵15. Hothorn T, Zeileis A. partykit: A modular toolkit for recursive partytioning in R. J Mach Learn Res. 2015;16(118):3905–9. Available from: https://jmlr.org/papers/v16/hothorn15a.html
https://jmlr.org/papers/v16/hothorn15a.h... ), described by Breiman et al. (¹⁷17. Breiman L, Friedman J, Stone CJ, Olshen RA. Classification and regression trees. Boca Raton, FL: Chapman and Hall/CRC; 2017.). According to Xiaogang and Chih-Ling (¹⁸18. Xiaogang S, Chih-Ling T. Tree-augmented Cox proportional hazards models. Biostatistics 2005;6(3):486–99. https://doi.org/10.1093/biostatistics/kxi024
https://doi.org/10.1093/biostatistics/kx... ), the tree-augmented Cox model assesses and remodels the inadequacies of the classical Cox model; it also adds new understandings of cancer death that were not exposed by the previous Cox regression analysis.

This study focuses on the analysis, through analytical methods, of which variables interfere in the increase in mortality from breast cancer in the region of Campina Grande, located in the State of Paraiba, Brazil. Additionally, the factors that favor the occurrence of censoring favored the process of remission. This fact is justified to aid decision-making for public policies, aiming to reduce the negative impact of the disease.

Thus, the objective of this study was to evaluate the relationship between covariates and time to death of patients with breast cancer, as well as the determination discriminatory power in the conditional inference tree of patients who had cancer.

MATERIALS AND METHODS

This was a retrospective cohort study, with data collected from the medical records of women who had breast cancer.

Sampling

In the simple sample random method, the premise is that each component of the population studied has the same chance of being chosen to compose the sample. The technique that guarantees this equal probability is the random selection of individuals; for example, by drawing lots (¹⁹19. Levy PS, Lemeshow S. Sampling of populations: methods and applications. Hoboken, NJ: John Wiley & Sons; 2013.). The equation below shows the calculation for the sample.

In the equation, n is the number of individuals in the sample, N is the estimated population size, p is the population proportion of individuals who belong to the category of interest to be studied, q is the population proportion of individuals who do not belong to the category that the study is interested in, Z_α/2 is the value of the significance level α, and E is the margin of error or the maximum estimation error. According to Yu et al. (²⁰20. Levine DM, Berenson ML, Stephan D. Estatística: teoria e aplicações. Rio de Janeiro: LTC; 2000.), when the population parameters p and q are not known, the sample parameters, p^ and q^ are not known either, and the author recommends replacing them by 0.5. So, the formula for calculating the sample size is:

Data collection

Data were obtained from the medical records of patients with breast cancer who underwent treatment at an oncology reference hospital in Campina Grande, State of Paraiba, Brazil, between 2005 and 2015. On average, approximately 200 women underwent breast cancer treatment per year in this hospital. Thus, taking into account the α level of significance of 5% and the margin of error of 7.5%, the minimum sample size should be 158 observations. In this study, 161 observations were used.

The retrospective study was carried out with authorization from the ethics committee (Certificado de Apresentação para Apreciação Ética—CAAE) of the Federal University of Campina, number 97198518.9.0000.5182. In the data collection, the medical records of patients who had breast cancer and underwent treatment at the hospital were anonymized in accordance with Brazil’s New Data Law (nova lei de proteção de dados—LGPD). Information was collected directly from medical records, chosen randomly to obtain a probabilistic sample, and so it was not necessary to obtain free and informed consent of the participants. The hospital’s approval was requested, as the research was carried out on secondary data (patient records).

The variables collected were: date of the first appointment; date of last appointment; date of patient’s death; age; number of doses of hormone therapy, chemotherapy, and radiotherapy; type of tumor; and molecular markers: estrogen receptor, progesterone receptor, Ki67 protein, P53, and HER2.

Patients were categorized by time until death, which was calculated from the date the woman visited the hospital for the first time until the date of her death. The censoring time was the days between the date of admission to the hospital and the date of the last consultation; those patients who did not obtain the event of interest by the end of the study were considered as censored. Hence, the database can be divided into two groups: group 1, comprising those patients who were not censored, due to remission or discontinuation of treatment; and group 2, comprising patients who died due to breast cancer.

Survival analysis

Survival analysis is a branch of statistics that analyzes times until the occurrence of a given event: time that an individual survives a given treatment; time until the development of a disease; or simply time until death (¹²12. Colosimo E, Giolo S. Análise de sobrevivência aplicada. 1 ed. São Paulo: Editora Edgard Blucher; 2006., ¹⁴14. Collett D. Modelling Survival Data in Medical Research. Boca Raton, FL: CRC Press; 2015.). According to Yu et al. (²¹21. Yu Z, Zhou X, Liu S, Wang X. Cox Proportional Risk Model and Its Application in Environmental Survival Analysis. In: Wang T-S, Ip AWH, Tavana M, Jain V, editors. Recent Trends in Decision Science and Management. Singapore: Springer; 2020.), the response variable corresponds to the time until the occurrence of an event of interest. Survival data sets are characterized by failure times, whose important characteristic is the presence of censoring, which represents the partial observation of the response (²²22. Nikulin M, Wu HI. The Cox model and its applications. Berlin: Springer; 2016., ²³23. Deo SV, Deo V, Sundaram V. Survival analysis—part 2: Cox proportional hazards model. Indian J Thorac Cardiovasc Surg. 2021;37:229–33. https://doi.org/10.1007/s12055-020-01108-7
https://doi.org/10.1007/s12055-020-01108... ).

The Kaplan–Meier estimator stands out for estimating survival curves (²³23. Deo SV, Deo V, Sundaram V. Survival analysis—part 2: Cox proportional hazards model. Indian J Thorac Cardiovasc Surg. 2021;37:229–33. https://doi.org/10.1007/s12055-020-01108-7
https://doi.org/10.1007/s12055-020-01108... ). The Kaplan–Meier estimator allows for testing hypotheses that do not require assumptions about the distribution of data (²⁴24. Kaplan EL, Meier P. Nonparametric estimation from incomplete observations. J Am Stat Assoc. 1958;53(282):457–81. https://doi.org/10.2307/2281868
https://doi.org/10.2307/2281868... ). It analyzes data measured only on an ordinal scale, which can occur for categorized data measured on a nominal scale and allow the estimation of the survival function incorporating censoring (²⁵25. Zhou M. Empirical likelihood method in survival analysis. Boca Raton, FL: Chapman and Hall/CRC; 2019., ²⁶26. Ng S. Mixture modelling for medical and health sciences. Boca Raton, FL: CRC Press; 2019.). The survival function estimated by Kaplan–Meier considers the occurrence of distinct failures in time intervals, where the survival times are ordered; that is, t₁ ≤ t₂ ≤ t₃ ≤...≤ t_k, and more than one failure may occur at the same time:

1. i. t₁ ≤ t₂ ≤ t₃ ≤...≤ t_k, distinct and ordered times of failures;

2. ii. d_j, number of failures up to time t _j, j=1,2,...,k;

3. iii. n_j, the number of items at risk; that is, individuals did not fail and were not censored until t_j.

According to Ng (²⁶26. Ng S. Mixture modelling for medical and health sciences. Boca Raton, FL: CRC Press; 2019.), the Kaplan–Meier estimator Sˆ(t) is defined by:

where t₀ is the longest time failure less than t.

Cox model

The model presented by Cox (²⁷27. Cox DR. Regression models and life-tables. J R Stat Soc Series B Stat Methodol. 1972;34(2):187–202. https://doi.org/10.1111/j.2517-6161.1972.tb00899.x
https://doi.org/10.1111/j.2517-6161.1972... ) is the most used in clinical studies due to its versatility. The survival time does not need to follow a probability distribution and the structure of this model has a nonparametric and a parametric component, justifying its denomination as a semiparametric model (²¹21. Yu Z, Zhou X, Liu S, Wang X. Cox Proportional Risk Model and Its Application in Environmental Survival Analysis. In: Wang T-S, Ip AWH, Tavana M, Jain V, editors. Recent Trends in Decision Science and Management. Singapore: Springer; 2020., ²²22. Nikulin M, Wu HI. The Cox model and its applications. Berlin: Springer; 2016.), and it is given by:

where g is a non-negative function specified such that g(0)=1. The term λ₀(t) is a non-negative function of time, representing the nonparametric component of the model, which is not specified. This component is usually called the base or basal function. The parametric component is often expressed by:

where β is the vector of parameters associated with p covariates. The Cox model has the proportional hazards assumption, which characterizes the failure rate of two different individuals over time to be constant over time. The survival function given the covariate vectors is given by:

with the basic survival function defined as:

Due to the nonparametric component, Cox (²⁷27. Cox DR. Regression models and life-tables. J R Stat Soc Series B Stat Methodol. 1972;34(2):187–202. https://doi.org/10.1111/j.2517-6161.1972.tb00899.x
https://doi.org/10.1111/j.2517-6161.1972... ) formalized the partial maximum likelihood method, eliminating the nonparametric component from the model.

Model selection

Akaike information criterion. The Akaike information criterion (AIC) seeks to adjust the most parsimonious model possible; that is, the model that involves the least probable parameters to be estimated and to explain the behavior of the variable as well as or even better than the response variable of the saturated model (²⁸28. Kimura K, Waki H. Minimization of Akaike's information criterion in linear regression analysis via mixed integer nonlinear program. Optim Methods Softw. 2018;33(3):633–49.).

According to Moore (²⁹29. Moore DF. Applied survival analysis using R. Springer; 2016.), one of the best ways to evaluate statistical models is via AIC, which calculates the likelihood of the model being penalized by the number of parameters. The objective is to find the model such that the AIC value is as small as possible, with this value calculated as:

where l(b) is the likelihood of the model and k is the number of parameters. For Kimura and Waki (²⁸28. Kimura K, Waki H. Minimization of Akaike's information criterion in linear regression analysis via mixed integer nonlinear program. Optim Methods Softw. 2018;33(3):633–49.), the inclusion of variables in the model causes a decrease in the AIC value; however, at some point the criterion starts to increase, indicating that the inclusion of particular variables is unnecessary and will not contribute to parameter estimates.

Variable selection. One of the most-used variable selection methods in survival analysis is stepwise (step-by-step selection), which is nothing more than a forward method adjustment (²²22. Nikulin M, Wu HI. The Cox model and its applications. Berlin: Springer; 2016., ³⁰30. Dessai, S, Simha V, Patil V. Stepwise cox regression analysis in SPSS. Cancer Res Stat Treat. 2018;1(2):167. https://doi.org/10.4103/CRST.CRST_7_19
https://doi.org/10.4103/CRST.CRST_7_19... ). The procedure has advantages if there are numerous potential explanatory variables, but it is also criticized because it can exclude clinical experience and knowledge in the model-building process (³¹31. Zhang Z. Variable selection with stepwise and best subset approaches. Ann Transl Med. 2016;4(7). https://doi.org/10.21037/atm.2016.03.35
https://doi.org/10.21037/atm.2016.03.35... ).

Decision tree. The conditional inference trees estimate a regression relationship by binary recursive partitioning in a conditional inference structure (³²32. Hothorn T, Hornik K, Zeileis A. Unbiased recursive partitioning: A conditional inference frame work. J Comput Graph Stat. 2006;15(3):651–74., ³³33. Hothorn T, Zelesi A, Hothorn MT. Package ‘partykit’. 2020.). The algorithm works in three steps. 1) It tests the value of the global hypothesis of independence between the input variables and the answer (which can also be multivariate), stopping the algorithm if it cannot reject the hypothesis. Otherwise, select the input variable with the strongest association with the answer. The p-value measures this association corresponding to a test for the partial null hypothesis of a single input variable and the answer. 2) It implements a binary division on the selected input variable. 3) It repeats steps 1 and 2 several times. The implementation uses a unified framework for conditional inference or permutation tests. The stopping criterion in step 1 is based on the p-values adjusted by the multiplicity of the univariate p-values (testtype = “Univariate”) of the partykit package (¹⁶16. Braga LCC, Drummond IN. Extração de informação em bases de dados abertas governamentais através de uma abordagem de mineração descritiva empregando a ferramenta R. Rev Informática Aplicada. 2018;14(1). https://doi.org/10.13037/ria.vol14n1.201
https://doi.org/10.13037/ria.vol14n1.201... ) of the R Core Team software (³⁴34. R Core Team. R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing; 2021. Available from: https://www.R-project.org/.
https://www.R-project.org/... ). This statistical approach ensures that the right-sized tree is grown without additional (post)pruning or cross-validation. The statistical analyses and graphics were performed using R/RStudio software version 4.1.1 (³³33. Hothorn T, Zelesi A, Hothorn MT. Package ‘partykit’. 2020.).

RESULTS

The results show that the mean age of the patients who were censored was approximately 61 years. The average service time until censoring was around 1 120 days. Half of the patients undergoing treatment received more than 52 doses of hormone therapy. The average number of chemotherapy sessions was approximately six sessions per patient, and about half of the patients had more than 27 radiotherapy sessions (Table 1).

Table 2 shows that the mean age of patients who died was approximately 58 years old. Regarding the length of care, the average number of days between the first consultation and death was 1 250 days, with half of the patients dying within 888 days after being admitted to the hospital. Half of the patients received more than five doses of hormone therapy and underwent more than 25 radiotherapy sessions. The average number of chemotherapies was approximately 19 sessions per patient.

Figure 1 shows the histogram of time to censoring and time to death. Thus, it is possible to notice that patients were censored more frequently in the first 500 days, while the frequency of patients who died was higher in 2 000 days.

To build the Cox model, the variables used were: location; age; number of doses of hormone therapy, radiotherapy, and chemotherapy; and estrogen and progesterone receptors, HER2, Ki-67, and p53. For the model containing all covariates, the AIC was 110.03. Only the variables number of hormone treatments and HER2 gene positive were significant in this model. Therefore, the stepwise regression variable selection criterion was used to obtain a more consistent model. This new model had an AIC equal to 98.63, which was relatively lower than the initial model, and all covariates were significant. We verified the proportional hazards assumption for a Cox regression model fit (coxph) using the cox.zph function in R. We found that the variable number of radiotherapy treatments violated the assumption of proportionality. Thus, the stratified Cox model was used, a contiguous fact that the proportionality test of this new model was not significant (p = 0.09) and presented an AIC (35.75) lower than the models previously evaluated.

Figure 2 shows the survival curves for variables on tumor location and molecular markers.

The results presented in Table 3 highlight that with each addition of a hormone therapy unit, the patient’s risk of death decreased by 5.5%, and the risk of death for a patient with positive HER2 was 34.5% lower than those patients who were negative for this gene.

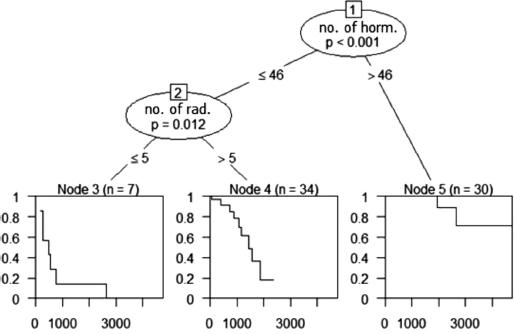
According to Figure 3, the variables number of hormone therapy units and number of radiotherapy presented a high discriminatory power in the conditional inference tree; they also are responsible for the division of nodes, generating branches that are nodes (branches 3, 4, 5). Thus, those patients who had more than 46 hormone therapies performed during treatment have a better cure prognosis (node 5), with a median time of 4753 days, and probably the high incidence of censoring (about 70%) is due to loss to follow-up because of prolonged treatment.

On the other hand, those patients who underwent fewer than 46 hormone therapies and had fewer than five radiotherapies performed had the worst prognosis, with a median lifespan of 490 days. Those who underwent fewer than 46 hormone therapies and had more than five radiotherapies performed had an intermediate prognosis, with a median lifespan of 1 446 days.

DISCUSSION

The number of chemotherapy sessions performed in women in the censored group was lower than in women who died. Although chemotherapy is one of the efficient ways to treat breast cancer, some studies correlate the number of chemotherapy sessions with the severity of the disease. These results are similar to those found in a study carried out in Canada (³⁵35. Budhwani S, Moineddin R, Wodchis W, Zimmermann C, Howell D. Do Longitudinally Collected Symptom Scores Predict Time to Death in Advanced Breast Cancer: A Joint Modeling Analysis. J Pain Symptom Manage. 2020;59(5):1009–18. https://doi.org/10.1016/j.jpainsymman.2019.12.006
https://doi.org/10.1016/j.jpainsymman.20... ) with 993 patients and evaluating the symptom scores of patients undergoing breast cancer treatments, suggesting that women with more than three-year survival need more aggressive treatment, developing a greater burden of symptoms than those who died in under three years. The log-rank test showed that the estrogen receptor (p < 0.001), progesterone receptor (p = 0.003), and HER2 (p = 0.003) variables showed a significant difference concerning the categories; and women classified as triple-negative—for estrogen receptor, progesterone receptor, and HER2—had a shorter survival time compared to women who were positive for these characteristics. This is because women with triple-negative subtype do not benefit from hormonal therapies or immunotherapies, but instead depend exclusively on surgery, more aggressive chemotherapy, and radiotherapy, and so they have a worse prognosis and shorter survival (³⁶36. Waks AG, Winer EP. Breast Cancer Treatment: A Review. JAMA. 2019;321(3):288–300. https://doi.org/10.1001/jama.2018.19323
https://doi.org/10.1001/jama.2018.19323... ).

Those patients with HER2 overexpression presented the worst prognosis, as it is an accelerated tumor growth factor. Nonetheless, there is a specific immunotherapy for these women, which is recommended for HER2 factor/neu inhibition and is also used in patients with metastases (³⁷37. Kreutzfeldt J, Rozeboom B, Dey N, De P. The trastuzumab era: current and upcoming targeted HER2+ breast cancer therapies. Am J Cancer Res. 2020;10(4):1045–67.). In this regard, the incorporation report prepared by the Ministry of Health of Brazil (³⁸38. Conitec. Relatório Terapia-alvo imunoterapia. Brasília: Ministério da Saúde; 2019.) suggests that immunotherapy has an advantage in the treatment of patients with melanoma at any stage when compared to target therapies. Notwithstanding, its cost remains high, preventing its implementation for the treatment of patients with advanced, non-surgical, and metastatic melanoma (³⁸38. Conitec. Relatório Terapia-alvo imunoterapia. Brasília: Ministério da Saúde; 2019.).

The results indicated that the longer the woman’s survival, there is possibly a worsening of the quality of life, related to the therapies offered. As the disease progresses, treatment goals can be modified to focus on the comfort of the patient, such as providing palliative care to ensure a better quality of life (³⁹39. Cherny N, Paluch-Shimon S, Berner-Wygoda Y. Palliative care: needs of advanced breast cancer patients. Breast Cancer. 2018;10:231–43.).

The survival models of decision tree analysis offer many advantages over Cox regression, such as explicit maximization of predictive accuracy, parsimony, statistical robustness, and transparency (⁴⁰40. Linden A, Yarnold PR. Modeling time‐to‐event (survival) data using classification tree analysis. J Eval Clin Pract. 2017;23(6):1299–308.). Therefore, researchers interested in rigorous predictions and clear decision rules should consider developing models using the survival framework of classification trees (⁴⁰40. Linden A, Yarnold PR. Modeling time‐to‐event (survival) data using classification tree analysis. J Eval Clin Pract. 2017;23(6):1299–308.). Weathers (⁴¹41. Weathers B. Comparison of Survival Curves Between Cox Proportional Hazards, Random Forests, and Conditional Inference Forests in Survival Analysis. All Graduate Plan B and other Reports. 2017;927. https://doi.org/10.26076/e209-46bd
https://doi.org/10.26076/e209-46bd... ) applied three techniques to five publicly available datasets and compared their fits using prediction error curves and the concordance index. The author identified “types of data” in which random survival forests and conditional inference trees (ctrees) may be expected to surpass the Cox model.

The limitations of this study include the lack of a date of diagnosis, which results in a gap of days between diagnosis and admission to hospital. In addition, the histological characteristics of the tumor were not taken into account, and these may have accelerated death in some women, as they indicate tumors that are more aggressive or do not respond to the chemotherapy applied. This status would be valuable in building on the results of this research.

Conclusion

We concluded that women with triple-negative molecular subtypes for breast cancer have a shorter survival time, correlated with others with positive hormone receptors.

The study presents a favorable scenario for the use of immunotherapy as a therapy for patients with HER2 overexpression. Due to its high cost, in Brazil’s Unified Health System (Sistema Único de Saúde—SUS) this therapy is only used in patients with HER2 or metastasis. Thus, further studies could assess the effectiveness of immunotherapy in patients with other conditions, as well as the cost-effectiveness for the SUS of implementing this treatment on a larger scale, to favor the prognosis and better quality of life for the patient.

Disclaimer.

Authors hold sole responsibility for the views expressed in the manuscript, which may not necessarily reflect the opinion or policy of the RPSP/PAJPH or the Pan American Health Organization.

REFERENCES

Publication Dates

History