ARTIGO ARTICLE

Introduction

The concerns of geographical epidemiology

The analysis of the geographical distribution of the incidence of disease and its relationship to potential risk factors has an important role to play in various kinds of public health and epidemiological studies. For the purposes of this paper this general area is referred to as "geographical epidemiology" and four broad areas of statistical interest are identified:

Disease Mapping focusses on producing a map of the true underlying geographical distribution of the disease incidence, given "noisy" observed data on disease rates. This may be useful in suggesting hypotheses for further investigation or as part of general health surveillance and the monitoring of health problems. For example, in assisting to detect the outbreak of a possible epidemic, or in identifying significant trends in disease rates over time, or in particular geographical localities.

Ecological Studies are concerned with studying associations between observed incidence of disease and potential risk factors as measured on groups rather than individuals, where these groups are typically defined by geographical areas. Such studies are valuable in investigating the aetiology of disease and may help to target further research, and possibly preventative measures.

Disease Clustering Studies focus on identifying geographical areas with significant elevated risk of disease, or on assessing the evidence of elevated risk around putative sources of hazard. Uses include the targeting of follow up studies to ascertain reasons for identified clustering in disease occurence, or the initiation of control measures where the aetiology of identified clustering is established.

Environmental Assessment and Monitoring is concerned with ascertaining the spatial distribution of environmental factors relevant to health and exposure to these, so as to establish necessary controls or take preventative action.

Sub-areas exist under any one of these four main headings depending on the particular epidemiological or public health context and upon whether data is available on individual cases of a disease, or only at the level of geographical area, and upon whether there is a temporal as well as a spatial dimension to the analysis. The distinction between the four main types of study is also somewhat blurred in practice. For example, good disease incidence maps often play an important preliminary role in studies of disease clustering, disease mapping commonly incorporates relationships with covariates representing known risk factors for the disease, and putative hazards are sometimes usefully viewed as particular kinds of covariate in the analysis, while environmental assessment may well be the prelude to a study designed to investigate whether there is a relationship between some suspected risk factor and disease incidence.

These provisos accepted, the division of geographical epidemiological concerns into four main areas provides a useful structure under which to review associated statistical methods in the subsequent sections of this article. At the same time it should be appreciated that although the focus of this paper is on geographical epidemiology, the concerns discussed under these four headings can be extended to a broader public health context; for instance, in planning the location of health services based on relative risk, in estimating immunization coverage, or in assisting to design other forms of disease prevention or health education programs. We do not explicitly comment on these broader uses, but they should be borne in mind in relation to the spatial methods subsequently discussed.

Statistical methods in geographical epidemiology

Given the breadth and importance of the concerns in geographical epidemiology, as outlined in the previous section, it is not surprising that there has been considerable interest in the area in recent years. Much of this interest has been in the development of relevant statistical methods and techniques and there is no doubt that this particular vein of research has been, and continues to be, a fruitful source of interesting statistical problems, motivating successful methodological developments within that discipline.

Several issues of major statistical journals have been devoted to spatial statistical methods in health applications (e.g. American Journal of Epidemiology, 132: S1-S202 - 1990; Journal of Royal Statistical Society, Series A, 152-1989; Journal of Royal Statistical Society, Series D, 47-1989; Statistics in Medicine, 12-1993, 14-1995, 15-1996. There has also been a considerable volume of papers in the field published separately, key journals including: American Journal of Epidemiology; Biometrics; Biometrika; Environmetrics; Journal of Environmental and Ecological Statistics; Geographical Analysis; IEEE Transactions on GeoScience and Remote Sensing; Journal of Royal Statistical Society, Series A, B, C, & D; Journal of American Statistical Association; Mathematical Geology; Statistics in Medicine and Statistical Science. In addition a number of significant recent texts have been devoted to this subject area (e.g. Elliot et al., 1996; Gatrell & Loytonen, 1998; Halloran & Greenhouse, 1997; Lawson et al., 1999a)

There have also been various special initiatives concerned with statistical methods in geographical epidemiology. A notable example was the 1997 international workshop in Rome in conjunction with the European initiative on disease mapping and risk assessment and the WHO European Centre for Environment and Health (see Lawson et al., 1999a). Some of the work conducted under the European Spatial and Computational Statistics Network has also been particularly relevant to spatial epidemiology and this network has now held two international workshops (Aussois, France, 1998; Crete, Greece, 1999). In addition to these, a considerable amount of statistical work has been conducted under the aupices of other agencies with long term interests in geographical and environmental health issues, e.g. the Centres for Disease Control and Prevention (CDC); the Environmental Protection Agency (EPA); the National Research Centre for Statistics and the Environment; the Pan American Health Organization (PAHO); the World Health Organization (WHO) and various European Community government agencies.

The net benefits of the statistical efforts associated with all this activity are difficult to judge. Certainly we now have statistical tools that are capable of addressing much more complex situations than was the case say ten years ago. However, the epidemiological and public health implications and benefits arising from the use of such methods are more difficult to assess. This point is returned to in the final section of this article after looking at some of the statistical developments in more detail in preceding sections (each of which relates to one of the four main headings identified earlier and after considering the software environments which are available to implement methods discussed.

One general point worth making at this stage is that although certain of the four areas reviewed are characterized by specialized statistical methods, there is also considerable overlap in the statistical modelling that has been employed in any one of them. For example, "disease clustering studies" have given rise to an extensive and rather specialized literature on hypothesis tests for either "focussed" or "unfocussed" clusters of disease. "Environmental assessment" also inevitably involves a focus on specialised spatial interpolation methods, some of which are derived from the geostatistical literature. However, these kinds of exceptions aside, a distinctive feature of much of the recent modelling work in all areas is a Bayesian approach. Indeed, the various areas of geographical epidemiology have all provided a very fruitful area for the application of Bayesian models and associated Markov Chain Monte Carlo (MCMC) methodology. As will be seen in subsequent sections, the application of Bayesian techniques in Disease Mapping, in Ecological Studies, in Disease Clustering Studies and in Environmental Assessment and Monitoring is now well-established and accompanied by an extensive and growing literature.

Data types in geographical epidemiology

Before embarking on a review of methods under the four topic headings discussed earlier, it is useful to make some broad distinctions in the types of data that might have to be dealt with in any of these areas, since that will assist to further categorize the methods under each heading.

Broadly speaking, there are essentially four kinds of data which have to be considered. Some problems may involve simply one of these types of data, but often mixtures of data types may be involved. Some methods discussed in subsequent sections may only be appropriate to a specific data type, others may be able to be applied (or modified to apply) to more than one data type. The four data types are:

Irregular lattice data - measures aggregated/averaged to the level of census tracts or other type of administrative district. Could be counts of cases or population at risk, socio-economic measures, environmental assessments etc.

Case-event data - locations (usually residential) of individual cases of a disease, or of individual members of a suitable control group ("population at risk"). Covariates may also be measured on each individual.

Geostatistical data - measurements (usually of an environmental nature) sampled at point locations.

Regular lattice data - measures aggregated/averaged to a regular grid (typically arising from remote sensing).

In any of the above cases there could also be a temporal dimension as well as a spatial dimension to the data. For example, we might have case-event data on a disease where both the spatial location of cases and the time of onset of the disease is recorded. Environmental data is also often collected in both space and time.

Disease mapping

Maps of disease incidence have always played a key descriptive role in spatial epidemiology. They are useful for several purposes such as: identification of areas with suspected elevations in risk of a disease, assisting in the formulation of hypotheses about disease aetiology and assessing potential needs for geographical variation in follow-up studies, preventative measures, or other forms of health resource allocation.

From a statistical point of view the problem of disease mapping amounts to obtaining a "good" estimate of the geographic heterogeneity of the disease rate over the study area. The obvious approach is to map standardized rates, but many of the diseases of interest are relatively uncommon and observed SMRs therefore have high natural variability with extreme values tending to occur in areas with the smallest populations. The areas of greatest potential interest are thus often associated with the least reliable data. One therefore seeks methods to produce a more reliable map of the underlying geographical variation in disease rates which reduces excess local variability at the same time as correcting for variations produced by population age/sex variations or other well-known risk factors. Methodologically, there are conceptual similarities to general statistical techniques designed to "clean" observed spatial imagery.

Most commonly, the observed data on disease incidence is aggregated to an irregular lattice i.e. counts of cases and corresponding populations in area units. However, as health information systems steadily improve, there is an increasing demand for methods that can be used with case event data, where more precise locations of cases (usually residential addresses) are known. Models for the two different data types are dealt with separately below.

Mapping aggregated data

There are several different statistical approaches, but the focus here is on what has emerged as the "mainstream" methodology - that based on Bayesian hierarchical models. The basic model employed is that the observed counts of cases, y = (y₁ , . . . , y_n ), in the different areas, each follow a Poisson distribution with mean µ_i = e_{i ri} , where e_i is the "expected" number of cases in each area (based upon the population at risk and suitable overall reference rates for the disease) and r_i is the relative disease risk in area i.

Generally the "expected" number of cases e_i is assumed known and often incorporates stratification corrections for known confounders, such as age and sex (i.e. 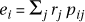, where r_j are known group overall reference rates and p_ij is the population of type j in area i). In the case of such "direct standardization", modelling often focusses on the log relative risk of the disease _.

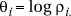If the q_i are taken as "fixed effects" then their maximum likelihood estimates are simply

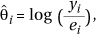
i.e. the relative risk estimates are just the traditional SMRs. But, as mentioned previously, SMRs in small areas may be unreliable because the most extreme SMRs are often based on only a few cases. Some "smoothing" of the raw SMRs is therefore incorporated into the model by taking the q_i as "random effects". Essentially this allows for overdispersion in the Poisson model caused by unobserved confounding factors (e.g. see Clayton & Bernardinelli, 1996; Mollié, 1995).

The most common method of estimating the vector of "random effects" q = (q₁ , . . . , q_n) is to adopt a Bayesian approach. Each q_i is assumed to arise from a suitable prior distribution with relevant "hyperparameters" each of which in turn arise from a suitably "non-informative" "hyperprior" distribution. Various specifications of the prior and hyperprior distributions are possible (e.g. see Bernardinelli et al., 1995a), but a typical choice in disease mapping is to take 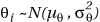with the non-informative hyperpriors being a normal distribution for the hyperparameter µ_qand a gamma distribution for the hyperparameter 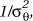with large variances in both cases. In general if P 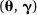denotes the chosen prior distribution involving a vector of hyperparameters g and if P (g) is the associated joint hyperprior, then the joint posterior distribution of all of the parameters given the data y is derived from the relationship:

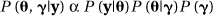
Given P 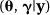, the parameters of interest, q, are then estimated from this posterior distribution via 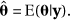Unfortunately, direct mathematical derivation of the posterior P 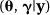from the above relationship involves a high-dimensional integration to obtain the constant of proportionality (the normalising constant) and is not mathematically tractable. Therefore, in practice, either empirical Bayes methods or Monte Carlo simulation is used to approximate P 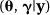indirectly.

In empirical Bayes (e.g. Clayton & Kaldor, 1987; Devine & Louis, 1994; Martuzzi & Elliott, 1996) the unknown vector of hyperparameters is replaced by suitable estimate 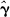. The problem of deriving the posterior then simplifies, since the corresponding relationship is now:

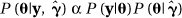
and this can be handled by direct mathematical analysis. Commonly, the hyperparameter estimates 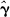that are used are their maximum likelihood estimates from the marginal likelihood 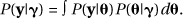In that case 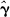is obtained from information pertaining to the overall map structure (hence the terminology "empirical" - the hyperparameters are estimated from global aspects of the same data set).

The problem with the empirical approach is that it makes no allowance for uncertainty in estimating g - the hyperparameters are simply replaced by their estimates assuming these to be error free (e.g. see Bernardinelli & Montmoli, 1992). In the MCMC approach the full hyperprior framework is used, but rather than attempt to determine P 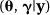by direct mathematical analysis, instead observations are indirectly simulated from this posterior using MCMC methods (e.g. see Brooks, 1998; Gilks et al., 1996). The desired parameter estimates 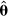are then calculated from relevant sample statistics of the simulated values from P 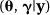. The basic idea of the MCMC approach is to simulate values from a Markov Chain whose equilibrium distribution is the same as the posterior distribution of interest. This is achieved via the general Metropolis algorithm which only requires the complex joint posterior distribution, P 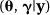, to be specified up to the normalizing constant (e.g. see Gilks et al., 1993). One particular variant of the general Metropolis algorithm known as "Gibbs sampling" (e.g. see Gilks et al., 1993) is convenient when conditional posterior distributions of each parameter given all the others are available up to a normalizing constant (as is the case here and often in spatial models more generally) see Gilks et al., (1993). Gibbs sampling is implemented in the BUGS or WinBUGS computer packages (Spiegelhalter et al., 1997) which provide a relatively easy way to fit a large range of Bayesian models. It consists of visiting each parameter in turn (i.e. here each 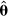_i in q and each hyperparameter in g) and simulating a new value for this parameter from its full conditional distribution given the current values for the remaining parameters (i.e. here from 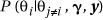etc.)

Regardless of which particular variant of the Metropolis algorithm is adopted, after discarding a suffcient number of initial "burn in" simulations the MCMC approach results in repeated sets of simulated values for the parameters 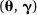from their posterior distribution P 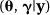. Samples from the marginal distributions 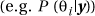are then approximated by simply picking out the values for one parameter from the simulated samples for 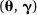ignoring the other parameters. Point estimates concerning the parameter are then obtained from the sample mean, of that set of values.

The basic model for relative risk that has been considered so far allows for Poisson overdispersion in the distribution of disease counts y_i via the random effects q_i. This may partially account for unmeasured covariates that induce spatial dependence in the y_i , but it does not allow for explicit spatial dependence between the y_i. The latter may be present (e.g. see Clayton et al., 1993) arising, for example, through lesser variability of rates in neighboring densely populated urban areas as opposed to sparsely populated rural areas, or through an infectious aetiology of the disease. Such explicit spatial dependence may be incorporated into the model by including an additional spatially structured random effect term (e.g. see Clayton & Bernardinelli, 1996; Mollié, 1995). The model is extended to: log µ_i = log e_i + q_i + n_i , so that now the log relative risks are given by q_i + n_i. The priors and hyperpriors relating to q_i are as before. But n_i are taken to have a spatially structured prior. A typical choice is to use a conditional intrinsic Gaussian autoregressive model (an example of a CAR, see Besag & Kooperberg, 1995) where:

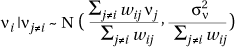
where w_ij are suitably chosen proximity weights for the areas (often simply 1 if two areas are adjacent, 0 otherwise) and the new hyperparameter s_n controls the strength of local spatial dependence. Typically a vague gamma hyperprior is assumed for 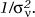MCMC methods then provide samples from P 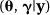where now g = (µ_q , s_q , s_n).

Further extensions to the disease mapping model are possible to include covariates which correct for known risk factors other than those incorporated into the direct standardization term (i.e. the expected cases e_i ). In that case, the model essentially becomes similar to that used in ecological investigations (see Section Ecological Studies). Indirect standardization is also one example of this, where population values in age/sex groups are treated as covariates in the model with associated unknown overall group reference rate parameters and this replaces the known "expected" number of cases e_i . The group reference rates are then estimated as part of the model.

Mapping case event data

Again various approaches exist, but generally there has been less work in this area than on aggregated data and a "mainstream" methodology is more difficult to identify. The basic model usually adopted is that locations of individual cases and of individuals in the population at risk both arise as inhomogenous Poisson processes with spatially varying intensities (events per unit area) denoted by µ(s) and p(s) respectively, where s represents spatial position. Then:

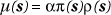
where a is the overall reference rate for the disease and r(s) is the relative risk surface. Often interest focusses on the estimation of log relative risk q(s) = log r(s) rather than directly on r(s).

A typical practical situation is that data are available on n = n₁ + n₂ point locations which correspond to n₁ cases of the disease at locations (s₁ , . . . , s_n1 ) and n₂ cases of a suitable control group at locations (s_n1+1 , . . . , s_n ). The control group may be primary data, or secondary data obtained by appropriate simulation of the location of control cases from socio-demographic data aggregated to small areas covering the region concerned. Given this data structure, a straightforward approach (see Bithel, 1990; Kelsall & Diggle, 1995) is then to non-parametrically estimate q(s) (to within an additive constant) via a log ratio of Kernel estimates as:

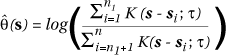
where K(.) is some suitable radially symmetric kernel function and t is a suitably chosen bandwidth.

Choise of an optimal bandwidth t is however rather difficult in the above approach (see Kelsall & Diggle, 1995) and more recent work (Kelsall & Diggle, 1998) avoids that problem by adopting a non-parametric binary regression approach which results in an indirect estimate of q(s). Essentially the method is to attach binary values y_i to all n data locations such that y_i = 1 if the location corresponds to a disease case and y_i = 0 if it does not. The probability that any point is a disease case, f(s), is then estimated via kernel regression (e.g. see Green & Silverman, 1994) of y_i on s_i i.e. by:

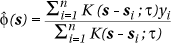
Then (to an additive constant) 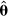(s) is given by logit 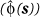i.e. by

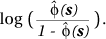
Bandwith selection methods are then easier to handle and the approach can also be extended to include covariates measured on each individual so as to correct for additional known risk factors for the disease. This is achieved via a Generalised Additive Model (GAM) as discussed later in the Section Ecological Studies.

Further issues and approaches in disease mapping

There are several further extensions and variations on the basic ideas used in disease mapping. This section lists some of the most significant issues that have been considered with relevant references.

General methods for simple exploratory analyses of spatial data which may be usefully applied in relation to disease incidence have been investigated by several authors (e.g. Cislaghi et al., 1995; Haining et al., 1998; Unwin & Unwin, 1998; Walter, 1993b; Wilhelm & Steck, 1998). The addition of further covariates to further refine the basic disease mapping model has already been mentioned (e.g. see Bernardinelli et al., 1997; Clayton & Bernardinelli, 1996; Clayton et al., 1993; Martuzzi & Elliott, 1996; Mollié, 1995; Muller et al., 1997; Xia et al., 1997). Several authors have also considered how models can be extended to handle disease incidence data which has a temporal, as well as a spatial dimension (e.g. Bernardinelli et al., 1995b; Knorr-Held & Besag, 1998; Waller et al., 1997). Special problems introduced by edge effects in disease mapping have been discussed by Lawson et al. (1999b). Bayesian mixture or latent structure models have also been used in disease mapping as an alternative to the more conventional models discussed earlier (e.g. Richardson & Green, 1997; Schalttmann & Bohning, 1993). Some other studies have also considered the application of geostatistical interpolation models (primarily variants of "kriging") to the analysis of disease rates (e.g. Carrat et al., 1992; Webster et al., 1994).

Ecological studies

As mentioned previously, "ecological studies" are concerned with studying associations between observed incidence of disease and potential risk factors as measured on groups rather than individuals, where these groups are typically defined by geographical areas or location. Such studies are valuable in investigating the aetiology of disease and may help to target further research and possibly preventative measures.

From a statistical point of view ecological studies involve regression type models, but the models are complicated by the need to allow for both spatial and aspatial confounding factors (see Clayton et al., 1993; Prentice & Sheppard, 1995; Richardson et al., 1992). Usually such studies involve observed data on disease incidence which is aggregated to an irregular lattice i.e. counts of cases and corresponding populations in areal units. However, more recently there has also been some work studying associations between suspected risk factors and disease incidence using case event data or mixtures of aggregated data (relating to risk factors) and individual data (relating to disease incidence). Models for aggregated disease incidence data and for that which involves case events are dealt with separately below. The aggregated nature of the data normally involved in ecological studies has led to considerable emphasis on the need to avoid, and if possible, correct for the so-called "ecological fallacy" i.e. the various forms of bias associated with making inference about the effects of factors on the disease risk of individuals from relationships obtained on groups where within group variability cannot be assessed (e.g. see Axelson, 1999; Elliot et al., 1996; Prentice & Sheppard, 1995).

Models for aggregated data in ecological studies

As in disease mapping, several different approaches have been used. The one that tends to dominate in the literature uses extensions to the Bayesian hierarchical models employed in disease mapping and the focus here is mostly on that framework. It should be noted however, that other forms of spatial regression model have also been adopted, some of which have potential advantages in terms of addressing ecological bias and that point is returned to in Section Further Issues and Approaches in Ecological Studies.

The basic Bayesian hierarchical model adopted is a straightforward extension of that discussed under disease mapping. Now K covariates, (x_i1 , . . . , x_iK), are included and related to suspected risk factors measured in each area, so that the model becomes:

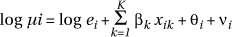
with µ_i, e_i, q_i, n_i as in Section Mapping Aggregated Data and b_k are new parameters reflecting the influence of each covariate on the log relative risk which is now modelled as 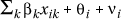. As mentioned previously, one could drop the "direct standardization term", log e_i , and instead use indirect standardization by incorporating a constant b₀ and including amongst the covariates relevant measures of population age/sex structure.

The priors and hyperpriors for q_i and n_i are chosen as in Section Mapping Aggregated Data. The new parameters, b, are each taken to have specified "non-informative" priors (e.g. Normal distributions with large variances). We then proceed as before using MCMC methods to derive samples from the posterior 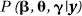with g referring, as earlier, to the vector of hyperparameters relating to the random effects q_i and n_i. Further details and variations on this basic modelling framework may be found in many published examples of ecological studies (e.g. see Bernardinelli et al., 1997; Clayton et al., 1993; Lawson et al., 1999a; Mollié, 1995; Richardson et al., 1992; Rushton et al., 1996; Spiegelhalter, 1998)

Models for case event data in ecological studies

There has been relatively little work in this area compared with that devoted to aggregated disease incidence data. Some recent initiatives include work by Kelsall & Diggle (1998) and Lawson & Clark (1999). The latter work was mentioned in passing in relation to disease mapping in Section Mapping Case Event Data. It involves the extension of the non-parametric binary regression model considered there to a GAM. Recall that in the model discussed previously the focus was on estimation of f(s), the probability that any point is a disease case in a combined realization of cases and controls, the log relative risk surface, q(s), is then related to this (up to an additive constant) by logit (f(s)). When additional risk factors are involved then instead of estimating f(s) by kernel regression, K covariates are included, (x₁(s), . . . , x_K(s)), in the regression, so that the data y_i are observations on a binary response variable ("case or not case") with associated probability f(s) such that:

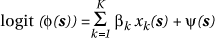
If y(s) is assumed to be a "smooth" function of s, then the above represents a GAM with a logit link function. GAMs are fitted by an iteratively weighted additive model procedure (see Hastie & Tibshirani, 1990) that is implemented in several software packages (e.g. Splus - Vernables & Ripley, 1994) Alternative ways of handling associations between suspected risk factors and disease incidence using case event data are discussed in Best et al. (1998); Lawson & Clark (1999) and Lawson et al. (1999a).

Further issues and approaches in ecological studies

Several further extensions and variations on the basic models used in ecological studies have been investigated. This section lists some of the most significant issues that have been considered with relevant references.

The general approach of graphical models (e.g. Spiegelhalter, 1998) provide a particularly valuable framework within which to specify the dependency structure of hierarchical Bayesian ecological models. Corrections to adjust for measurement error in the covariates have been suggested by Bernardinelli et al. (1997). Mixtures of case event and aggregated data have been discussed by Best et al. (1998) and Plummer & Clayton (1996). Thomson et al. (1999) has considered a situation involving aggregated data corresponding to a mix of different geographical scales. Bayesian latent structure or mixture models have also been employed in ecological studies as an alternative to the more conventional model discussed in Section Models for Aggregated Data in Ecological Studies (e.g. Schalttmann et al., 1996; Weir & Pettitt, 1999). Multi-level models (Goldstein, 1995) have also been employed as an alternative to the Bayesian approach (e.g. Congdon, 1998; Langford & Lewis, 1998). Other forms of spatial regression models have also been adopted (Brunsdon et al., 1998; Christiansen & Morris, 1997; Ghosh et al., 1998; Prentice & Sheppard, 1995; Wolpert & Ickstadt, 1998; Yasui & Lele, 1997) Some of these involve so-called "aggregated models" which are particularly orientated to reducing ecological bias by combining partial samples of individual level data on risk factors in addition to that on groups at the areal level. Ecological models appropriate for spatio-temporal data have also been considered (e.g. Bernardinelli et al., 1995b; Knorr-Held & Besag, 1998; Waller et al., 1997; Wikle et al., 1998). Methods for longitudinal data in general (e.g. see Diggle et al., 1994) have also been applied in ecological studies.

Disease clustering studies

As mentioned earlier, disease clustering studies seek to establish significant "unexpected" elevated risk of a disease either in space, or in space and time. Such localized "clusters" could arise from many factors e.g. an unidentified infectious agent, localized pollution sources, or localized common treatment side effects. There are several comprehensive general reviews of the area (e.g. Alexander & Boyle, 1996; Alexander et al., 1991; Anderson & Titterington, 1997; Bithell, 1995; Hills & Alexander, 1989; Kulldorf & Nagarwalla, 1995; Olsen et al., 1996).

In general, disease cluster studies may seek to investigate a "general tendency to cluster" (no prespecified locations or number of suspected hazards) or be concerned with "focussed clustering" (prespecified number and locations for putative hazards). The two situations are discussed separately below. Note that the second situation naturally provides for a more powerful statistical test of the suspected clustering because the hypothesis is more tightly specified. However, there is a clear need to avoid what is sometimes referred to as "centering the target where the bullet strikes" which in this context would imply using the data to explore where elevations in risk appear to exist and then subsequently using those locations in a test of "focussed clustering".

In general, disease clustering studies may involve either case event or aggregated data (see Diggle & Elliott, 1995, for a discussion of the relative merits). In both cases known population heterogeneity and other covariates must be allowed for along with any natural tendency to cluster through effects induced by data aggregation or inadequately measured covariates.

Assessment of general clustering

A large amount of work in this area has focussed on development of hypothesis tests for a general tendency to cluster. Some of the most commonly used tests with associated references are listed below.

For aggregated data, the key hypothesis testing approaches suggested include those discussed by: Alexander et al. (1991); Assunção & Reis (1999); Besag & Newell (1991); Kulldorf (1997); Kulldorf & Nagarwalla (1995); Kulldorf et al. (1997); Oden (1995); Potthoff & Whittinghill (1966); Tango (1995); Turnbull et al. (1990); Walter (1993a, 1994); and Wittemore et al. (1987). Many of these various tests are more or less refined variations on similar themes. Some are concerned only with assessment of a tendency to cluster, others also identify the locations where such clustering occurs. For case event data, key hypothesis tests include those discussed by: Anderson & Titterington (1997); Cuzick & Edwards (1990); Diggle & Chetwynd (1991); and Oppenshaw (1991); Again some of these are concerned only with assessment of a tendency to cluster, others also identify the locations where such clustering occurs. Hypothesis tests designed to detect spatio-temporal interaction include those discussed by: Baker (1996); Jacquez (1996b); Knox (1964); Kulldorf & Hjalmars (1999); Lawson & Viel (1995) and Mantel (1967).

The problem with many such hypothesis tests for general clustering is that positive results invariably leave subsequent questions unanswered - how many clusters are there? How big are they? Where are they? For that reason approaches to disease clustering which employ an explicit model have some advantages. Recent work by Lawson & Clark (1999) typifies that kind of approach. In the case event situation they suggest extending the kind of case event model discussed in relation to disease mapping in Section Mapping Case Event Data to:

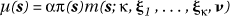
where, as before, µ(s) is the intensity of disease cases, p(s) is that of the population at risk and a is an overall disease rate, but now the previous unknown relative risk surface r(s) is replaced by the specified function m(·) which is parameterised in terms of an unknown number of clusters, k, a corresponding unknown set of cluster locations, (x₁ , . . . , x_k ), and a set of further parameters, n, which relate to the risk decay around clusters.

For example, one possible specification for such a model might be:

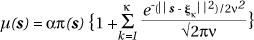
In that case, it has been suggested that p(s) be estimated from a set of controls using non parametric density estimation with a suitable bandwidth t(t can be derived separately or considered an additional unknown parameter in the Bayesian framework). Given such an estimate, 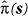, MCMC methods are then used to estimate the joint posterior for all the remaining unknown parameters involved. Note that since the number of parameters depends on k, which is itself a parameter, then this model is like a Bayesian mixture model with an unknown number of components and "reversible jump" MCMC sampling must be used (e.g see Richardson & Green, 1997). This model for case event data can be further generalized to allow for covariates and random effects in m(·). It can also be adapted for use with aggregated data consisting of counts y_i in areas A_i with means µ_i via:

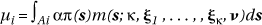
Details of how this is handled in a MCMC framework are provided in Lawson & Clark (1999) and Lawson et al. (1999a).

Assessment of focussed clustering

As for general clustering, several hypothesis tests for focussed clustering have been proposed. Some of the most commonly used tests with associated references are listed below.

For aggregated data, key hypothesis testing approaches for focussed clustering include those discussed by: Besag & Newell (1991); Stone (1988) (the focussed version of the general clustering test); Bithel (1995); Lawson (1993); and Waller & Lawson (1995). Corresponding tests for case event data include those discussed by: Cuzick & Edwards (1990); Stone (1988) (the focussed version of the general clustering test); Diggle & Elliot (1995); Korie et al. (1998); and Lawson & Waller (1996).

Again explicit modelling approaches have advantages if it is possible to use them, and the kind of models discussed in Section Assessment of General Clustering can be used with prespecified cluster locations (e.g. see Lawson, 1995). In the simplest situation for case event data with a single putative source at known location S₀, a suitable model might take the form:

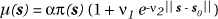
MCMC methods are then used to estimate n₁ and n₂ with p(s) estimated from a set of controls using non parametric density estimation with a suitable bandwidth t (t can be derived separately or considered an additional unknow parameter in the Bayesian framework). Extensions to include covariates can also be developed.

Earlier work by Diggle & Rowlingson (1994) and Diggle et al. (1997) uses a similar model, but avoids the density estimation of p(s) by focusing on the probability that an event is a disease case in the combined point process consisting of both cases and controls, as discussed previously in Section Maping Case Event Data. The model for a single source at known location s₀ is taken as:

where m(.) is a suitably chosen function to reflect risk decay around the source. As before, binary values y_i = 1 if point is a disease case and y_i = 0 if it is not. Then if

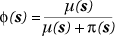
denotes the probabilty that any point is a disease case, we have:

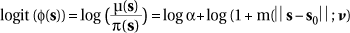
So p(s) has been "conditioned out" of the model and logistic regression with a binary response may be used to estimate the parameters n. This is a non-linear regression, but with a suitable choice of m(.) maximum likelihood estimation is relatively straightforward. Biggeri et al. (1996) provide details of a case study which employs this kind of model.

Further issues and approaches in disease clustering studies

There are several further extensions and variations relating to disease clustering studies. Some of the most significant issues that have been considered are listed below with relevant references.

Local indicators of association (e.g. Anselin, 1995; Getis, 1992) are general exploratory methods for spatial data which may have potential application in the preliminary phase of disease clustering studies. Models (rather than significance tests) that have relevance to spatio-temporal disease clustering investigation are discussed by Bernardinelli et al. (1995b); Knorr-Held & Besag (1998). Edge effect considerations in disease clustering are discussed by Lawson et al. (1999b). Cressie (1996) discusses inference for extreme values in general with relevance to cluster detection. Methods for incorporating directional or scale effects in the effects to be expected from putative sources of hazard have also been developed (e.g. Lawson & Viel, 1995; Waller & Turnbull, 1993). Jacquez (1996a) also discusses how uncertainy in the location of suspected sources of hazard may be handled.

Environmental assessment and monitoring

There are many known or suspected environmental factors that influence health (e.g. nuclear contamination, chemical toxins, air pollution, climatic or vegetation conditions that may influence distribution of disease vectors etc.). The quantity and quality of data on the environment is constantly increasing, particularly that from remote sensing platforms. Statistical models of environmental processes (e.g. see Piegorsch et al., 1998) allow spatial or spatio-temporal prediction of environmental factors which may then be used in conjunction with studies concerned with investigating disease aetiology or establishing public health intervention programmes (e.g. see Diggle & Richardson, 1993). The environmental processes under study usually exhibit strong local spatial, temporal and exogenous variability which needs to be allowed for in prediction models.

Environmental modelling is a very wide field and there is not space to discuss it in detail here. In general, remote sensing and image processing techniques increasingly play a key role (e.g. see Besag et al., 1991; Datcu et al., 1998; Schroder et al., 1998; Stein et al., 1998b) as do advances in modelling of Markov Random Fields (e.g. see Aykroyd, 1998; Cressie & Davidson, 1998; Tjelmeland & Besag, 1998). Many of the models used in environmental analysis adopt a Bayesian approach (e.g. see Besag & Green, 1993; Christakos & Li, 1998; Gaudard et al., 1999). In some cases there is a need to particularly focus on the prediction of threshold values of a phenomena in which case extreme value modelling (e.g. see Coles & Powell, 1996) may be necessary. Many studies involve spatio-temporal data (e.g. Kyriakidis & Journel, 1999; Stein et al., 1998a; Wikle et al., 1998). Other related areas include spatial sampling considerations (e.g. see Cox et al., 1997) and a need for versatile exploratory methods for spatial and space-time environmental data (e.g. Cook et al., 1997).

One recent general development concerning spatial prediction models is worthy of particular note here since it may have considerable potential in relation to health studies. The methodology of "kriging" in its many various guises (e.g. see Cressie, 1993), provides a versatile prediction tool for many geostatistical processes in space, or in space and time, and has usefully been employed in the prediction of environmental processes. However, kriging is conventionally concerned with prediction of Gaussian spatial or spatio-temporal process (e.g. it can over smooth when distribution is non-Gaussian). A significant recent development (Diggle et al., 1998) is the generalization of this methodology to situations in which data is non-Gaussian. The essential idea embeds linear kriging methodology within a non-linear and more general distributional framework, analogous to the embedding of standard least squares regression within the framework of generalized linear models (GLMs). A Bayesian approach, implemented through MCMC methods, is then used to fit the associated model. Diggle et al. (1998) provide details and applications of the approach.

Software in geographical / environmental epidemiology

A recurring theme in this paper is the computationally intensive nature of many of the statistical methods discussed. In this section some of the key software environments that exist to support the use of these methods are briefly discussed.

One computing environment which now dominates in much of the literature concerned with statistical methods in geographical epidemiology (as in many other areas of statistical analysis) is the versatile statistical computing language S-Plus (or the freely available public domain similar language R). A number of "add on" S-Plus packages particularly orientated to spatial applications are also available, in particular S+Spatial and S+GeoStat. The former includes several general purpose routines for spatial analysis, including point pattern analysis, some forms of spatial regression and simple kriging; whilst the latter is orientated more to geostatistical modelling. There are also a number of relevant public domain S-PLus libraries of functions supplied by third parties such as: SPLancs (point pattern analysis), geoS (geostatistical functions), Oswald (longitudinal data analysis) and spatial (basic spatial statistics). Many other relevant Splus functions (or groups of functions) are also available on the Internet from many individual contributors. Some of the above functionality is also available for R the public domain version of Splus.

S-plus or R do not in themselves provide for MCMC methods. Functionality in this area is provided by BUGS (Spiegelhalter et al., 1997) or, more recently, WinBUGs, both available in the public domain. These packages are able to implement many of the Bayesian models discussed in earlier sections of this paper. A public domain link between BUGS and S-plus also exists known as CODA which enables results from BUGS to be easily transferred to S-plus for subsequent analysis.

S-Plus, R and BUGS provide no direct ability to geographically visualize or map spatial results (although a Geo BUGS add-on is forthcoming). For that purpose it is necessary to use them in conjunction with a suitable Geographical Information System (GIS). The most commonly used packages in this regard in the health area are probably ARC/INFO and/or ARC/View (ESRI, 1996) and MapInfo (MapInfo Corporation, 1994). S-Plus provides a link to Arc/View which allows results to be transferred and mapped relatively easily. More special purpose computing packages for particular kinds of analysis relevant in geographical or environmental epidemiology include: ECOSSE (geostatistical/environmental modelling); DisMapWin (epidemiological mixture models - Schalttmann et al., 1996); MLWin (multi-level modelling); and Stat!, Gamma or SatScan (each relating to various types of spatial disease clustering tests and associated analysis). Full details of the various packages or libraries mentioned in this section are easily available through the Internet and those references are not repeated here.

Some closing remarks on statistical methods in geographical and environmental epidemiology

Given the rich variety of methods discussed in this paper, it is clear that the "state of the art" in statistical methods appropriate to certain problems in spatial epidemiology contains some powerful, versatile and useful tools. Research interest is strong and undoubtedly further developments and more sophisticated techniques will continue to develop. Many of the existing spatial methods and models are fairly widely known in the statistical community and some of them have been in use for several years. Spatial methods are less familiar amongst epidemiologists and public health specialists, but there are now a number of accessible texts, both on general introductory spatial analysis (e.g. Bailey & Gatrell, 1995), on more advanced spatial statistics (e.g. Cressie, 1993), on general statistical modelling (e.g. Venables & Ripley, 1994) and on MCMC methods (e.g. Gilks et al., 1996). These and similar texts, combined with the increasing amount of published work more specifically related to spatial epidemiology (as referenced in this paper), means that relevant methods and access to supporting software environments are now becoming better disseminated to health specialists. Hopefully that situation will continue to improve and spatial methods and models will be increasingly used where appropriate.

Reflection on the methods discussed in the paper does however reveal some areas which emerge as significantly "under played" amongst the "mainstream" methods and models. These include: a greater requirement for methods capable of handling mixtures of data types (e.g. at different levels of aggregation, or mixtures of case event and aggregated data, or a combination of information from remotely sensed imagery with that from more conventional health or demographic data sources); methods designed to better address the problem of ecological bias of various types; methods to better handle the spatio-temporal considerations present in many studies; the fact that there is currently a relative absence of methods designed to handle multivariate spatial responses; and also that the current spatial methods place a heavy reliance on the Euclidean distance metric combined with relatively crude topographic assumptions despite the potentially powerful functionality that GIS can now provide in that area.

Such areas provide a rich agenda for further study and some related exciting and diffcult challenges, particularly in the area of the multivariate study of groups of related diseases in spatial epidemiology and in incorporating more realistic and sophisticated measures of spatial proximity and spatial structure into models which appropriately exploit the detailed geographical information which is now available through GIS and remotely sensing.

In concluding this review of spatial statistical methods in health it is also appropriate to comment briefly on some wider and less statistical issues. The first point to acknowledge is that geographical epidemiology is epidemiology first and foremost and not statistics. Valuable spatial epidemiology does not necessarily follow from the use of better and more sophisticated statistical methods. Clearly, the ultimate benefits of all the statistical effort in geographical epidemiology also depends crucially on appropriate and well-founded epidemiological considerations combined with access to data at an appropriate level of detail and of suffcient quality to address the issues under consideration. The value of clear-cut, well designed geographical epidemiological studies associating disease with specific agents are not controversial. However, regardless of the sophistication of the statistical models employed, general geographical studies of widespread risk factors usually come up with relatively low relative risk estimates (resulting from low grade exposure, the diffculties of obtaining good exposure contrasts, and the problems of confounding effects). This can cause credibility problems for the results and limit their implications for public health response. For example, of the hundreds of "disease clustering" investigations conducted there are only a few examples of real "success" in terms of substantive advances in aetiological knowledge, or developments in public health (e.g. see Neutra, 1990).

Ultimately, geographical/environmental epidemiology needs to be evaluated in the same way as any other public health screening programs (e.g. see Axelson, 1999, Neutra, 1999). In some such applications which involve the spatial statistical analysis of already existing data, or that arise from routine collection systems, the "screening" is relatively cheap. However, this has to be balanced against the implications of false positive findings, the potential for effective intervention in cases of true positive findings, and the costs of the follow up and more focussed studies that will inevitably be necessary in such cases. Such considerations are important and whilst they do not mitigate against the development and use of improved statistical methodology, they do emphasize that the value of such methods has to be viewed in the context of a wider and ultimately more complex set of public health and epidemiological concerns.

References

ALEXANDER, F. E. & BOYLE, P., 1996. Methods for Investigating Localised Clusters of Disease. IARC Scientific Publication 135. Lyon: International Agency for Research on Cancer.         

ALEXANDER, F. E.; McKINNEY, P. A.; CARTWRIGHT, R. A. & RICKETTS, T. J., 1991. Methods of mapping and identifying small clusters of disease with applications to geographical epidemiology. Geographical Analysis, 23:156-173.         

ANDERSON, N. H. & TITTERINGTON, D. M., 1997. Some methods for investigating spatial clustering, with epidemiological applications. Journal of the Royal Statistical Society, Series A, 160:87-105.         

ANSELIN, L., 1995. Local indicators of spatial association - LISA. Geographical Analysis, 27:93-115.         

ASSUNÇÃO, R. M. & REIS, E. A., 1999. A new proposal to adjust Moran's I for population density. Statistics in Medicine, 18:2147-2162.         

AXELSON, O., 1999. The character and the public health implications of ecological analyses. In: Disease Mapping and Risk Assessment for Public Health (A. Lawson, A. Biggeri, D. Böhning, E. Lesaffre, J.-F. Viel & R. Bertollini, ed.), pp. 301-309, New York: Wiley and Sons.         

AYKROYD, R. G., 1998. Bayesian estimation for homogeneous and inhomogeneous Gaussian random fields. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20:533-539.         

BAILEY, T. C. & GATRELL, A. C., 1995. Interactive Spatial Data Analysis. Essex: Longman.         

BAKER, R. D., 1996. Testing for space-time clusters of unknown size. Journal of Applied Statistics, 23: 543-554.         

BERNARDINELLI, L.; CLAYTON, D. & MONTOMOLI, C., 1995a. Bayesian Estimates of disease maps: How important are priors? Statistics in Medicine, 14:2411-2431.         

BERNARDINELLI, L.; CLAYTON, D.; PASCUTTO, C.; MONTMOLI, C. & GHISLANDI, M., 1995b. Bayesian analysis of space-time variation in disease risk. Statistics in Medicine, 14:2433-2443.         

BERNARDINELLI, L. & MONTOMOLI, M., 1992. Empirical Bayes versus fully Bayesian analysis of geographical variation in disease risk. Statistics in Medicine, 11:983-1007.         

BERNARDINELLI, L.; PASCUTTO, C.; BEST, N. G. & GILKS, W. R., 1997. Disease mapping with errors in covariates. Statistics in Medicine, 16:741-752.         

BESAG, J. & GREEN, P. J., 1993. Spatial statistics and bayesian computation. Journal of the Royal Statistical Society, Series B, 55:25-37.         

BESAG, J. & KOOPERBERG, C., 1995. On conditional and intrinsic autoregressions. Biometrika, 82:733-746.         

BESAG, J. & NEWELL, J., 1991. The detection of clusters in rare diseases. Journal of the Royal Statistical Society, Series A, 154:143-155.         

BESAG, J.; YORK, J. & MOLLIÉ, A., 1991. Bayesian image restoration with two applications in spatial statistics. Annals of the Institute of Statistics and Mathematics, 43:1-20.         

BEST, N.; ICKSTADT, K. & WOLPERT, R., 1998. Spatial Poisson Regression for Health and Exposure Data Measured at Disparate Spatial Scales. Technical Report. London: Department of Epidemiology and Public Health, Imperial College School of Medicine.         

BIGGERI, A.; BARBONE, F.; LAGAZIO, C.; BOVENZI, M. & STANTA, G., 1996. Air pollution and lung cancer in Trieste: Spatial analysis of risk as a function of distance from sources. Environmental Health Perspectives, 104:750-754.         

BITHELL, J., 1990. An application of density estimation to geograhical epidemiology. Statistics in Medicine, 9:691-701.         

BITHELL, J., 1995. The choice of test for detecting raised disease risk near a point source. Statistics in Medicine, 14:2309-2322.         

BROOKS, S., 1998. Markov Chain Monte Carlo and its application. Journal of the Royal Statistical Society, Series D, 47:69-100.         

BRUNSDON, C.; FOTHERINGHAM, S. & CHARLTON, M., 1998. Geographically weighted regression - Modelling spatial non-stationarity. Journal of the Royal Statistical Society, Series D, 47:431-444.         

CARRAT, F. & VALLERON, A., 1992. Epidemiological mapping using the "kriging" method: Application to an influenza-like illness epidemic in France. American Journal of Epidemiology, 135:1293-1300.         

CHRISTAKOS, G. & LI, X. Y., 1998. Bayesian maximum entropy analysis and mapping: A farewell to kriging estimators? Mathematical Geology, 30:435-462.         

CHRISTIANSEN, C. & MORRIS, C., 1997. Hierarchical poisson regression modelling. Journal of the American Statistical Association, 92:618-632.         

CISLAGHI, C.; BIGGERI, A.; BRAGA, M.; LAGAZIO, C. & MARCHI, M., 1995. Exploratory tools for disease mapping in geographic epidemiology. Statistics in Medicine, 14:2363-2381.         

CLAYTON, D. & BERNARDINELLI, L., 1996. Bayesian methods for mapping disease risk. In: Geographic and Environmental Epidemiology: Methods for Small area Studies (P. Elliot, J. Cuzick, D. English, & R.Stern, ed.), pp. 205-220, Oxford: Oxford University Press.         

CLAYTON, D.; BERNARDINELLI, L. & MONTOMOLI, C., 1993. Spatial correlation and ecological analysis. International Journal of Epidemiology, 22:1193-1201.         

CLAYTON, D. & KALDOR, J., 1987. Empirical Bayes estimates of age-standardised relative risks for use in disease mapping. Biometrics, 43:671-681.         

COLES, S. G. & POWELL, E. A., 1996. Bayesian methods in extreme value modelling: A review and new developments. International Statistical Review, 64:119-136.         

CONGDON, P., 1998. A multilevel model for infant health outcomes: Maternal risk factors and geographic variation. Journal of the Royal Statistical Society, Series D, 47:159-182.         

COOK, D.; SYMANZIK, J.; MAJURE, J. J. & CRESSIE, N., 1997. Dynamic graphics in a GIS: More examples using linked software. Computers and Geosciences, 23:371-385.         

COX, D. D.; COX, L. H. & ENSOR, K. B., 1997. Spatial sampling and the environment: Some issues and directions. Environmental and Ecological Statistics, 4:219-233.         

CRESSIE, N., 1993. Statistics for Spatial Data. Chichester: Wiley.         

CRESSIE, N., 1996. Bayesian and constrained inference for extremes in epidemiology. In: American Statistical Association, Joint Meetings 1995, Epidemiology Proceedings, pp. 11-17. Alexandria: American Statistical Association.         

CRESSIE, N. & DAVIDSON, J. L., 1998. Image analysis with partially ordered markov models. Computational Statistics and Data Analysis, 29:1-26.         

CUZICK, J. & EDWARDS, R., 1990. Spatial clustering for inhomogeneous populations. Journal of Royal Statistical Society, Series B, 52:73-104.         

DATCU, M.; SEIDEL, K. & WALESSA, M., 1998. Spatial information retrieval from remote-sensing images - Part 1: Information theoretical perspective. IEEE Transactions on Geoscience and Remote Sensing, 36:1431-1445.         

DEVINE, O. & LOUIS, T., 1994. A constrained empirical Bayes estimator for incidence rates in areas with small populations. Statistics in Medicine, 13:1119-1133.         

DIGGLE, P. J. & CHETWYND, A., 1991. Second-order analysis of spatial clustering for inhomogeneous populations. Biometrics, 47:1155-1163.         

DIGGLE, P. J. & ELLIOTT, P., 1995. Disease risk near point sources: Statistical issues for analyses using individual or spatially aggregated data. Journal of Epidemiology and Community Health, 49:S20-S27.         

DIGGLE, P. J.; LIANG, K.-Y. & ZEGER, S. L., 1994. Analysis of Longitudinal Data. Oxford: Clarendon Press.         

DIGGLE, P. J.; MORRIS, S.; ELLIOTT, P. & SHADDICK, G., 1997. Regression modelling of disease risk in relation to point sources. Journal of the Royal Statistical Society, Series A, 160:491-505.         

DIGGLE, P. J. & RICHARDSON, S., 1993. Epidemiologic Studies of Industrial Pollutants - An introduction. International Statistical Review, 61:203-206.         

DIGGLE, P. J. & ROWLINGSON, B. S., 1994. A conditional approach to point process modelling of elevated risk. Journal of the Royal Statistical Society, Series A, 157:433-440.         

DIGGLE, P. J.; TAWN, J. A. & MOYEED, R. A., 1998. Model-based geostatistics. Journal of the Royal Statistical Society, Series C, 47:299-326.         

ELLIOTT, P.; CUZICK, J.; ENGLISH, D. & STERN, R., 1996. Geographic and Environmental Epidemiology: Methods for Small Area Studies. Oxford: Oxford University Press.         

GATRELL, A. & LOYTONEN, M., 1998. GIS and Health in Europe. London: Taylor and Francis.         

GAUDARD, M.; KARSON, M.; LINDER, E. & SINHA, D., 1999. Bayesian spatial prediction. Environmental and Ecological Statistics, 6:147-171.         

GETIS, A., 1992. Spatial interaction and spatial autocorrelation: A cross product approach. Environment and Planning A, 23:1269-1277.         

GHOSH, M.; NATARAJAN, K.; STROUD, T. W. F., & Carlin, B. P., 1998. Generalized linear models for small-area estimation. Journal of the American Statistical Association, 93:273-282.         

GILKS, W.; CLAYTON, D.; SPIEGELHALTER, D.; BEST, N.; McNEIL, A.; SHAPLES, L. & KIRBY, A., 1993. Modelling complexity: Applications of Gibbs sampling in medicine. Journal of the Royal Statistical Society, Series B, 55:39-102.         

GILKS, W. R.; RICHARDSON, S. & SPIEGELHALTER, D., 1996. Markov Chain Monte Carlo in Practice. London: Chapman and Hall.         

GOLDSTEIN, H., 1995. Multilevel Statistical Models. London: Edward Arnold.         

GREEN, P. & SILVERMAN, B., 1994. Non Parametric Regression and Generalised Linear Models. London: Chapman and Hall.         

HAINING, R.; WISE, S. & MA, J. S., 1998. Exploratory spatial data analysis in a geographic information system environment. Journal of the Royal Statistical Society, Series D, 47:457-469.         

HALLORAN, E. & GREENHOUSE, J., 1997. Statistics and Epidemiology: Environment and Health. New York: Springer-Verlag.         

HASTIE, T. & TIBSHIRANI, R., 1990. Generalised Additive Models. London: Chapman and Hall.         

HILLS, M. & ALEXANDER, F., 1989. Statistical methods used in assessing the risk of disease near a source of possible environmental pollution: A review. Journal of the Royal Statistical Society, Series A, 152:353-363.         

JACQUEZ, G. M., 1996a. Disease cluster statistics for imprecise space-time locations. Statistics in Medicine, 15:873-885.         

JACQUEZ, G. M., 1996b. A k-nearest neighbour test for space-time interaction. Statistics in Medicine, 15:1935-1949.         

KELSALL, J. E. & DIGGLE, P. J., 1995. Non parametric estimation of spatial variation in relative risk. Statistics in Medicine, 14:2335-2342.         

KELSALL, J. E. & DIGGLE, P. J., 1998. Spatial variation in risk of disease: A nonparametric binary regression approach. Journal of the Royal Statistical Society, Series C, 47:559-573.         

KNORR-HELD, L. & BESAG, J., 1998. Modelling risk from a disease in time and space. Statistics in Medicine, 17:2045-2060.         

KNOX, E. G.,1964. The detection of space-time interactions. Applied Statistics, 13:25-29.         

KORIE, S.; CLARK, S. J.; PERRY, J. N.; MUGGLESTONE, M. A.; BARTLETT, P. W.; MARSHALL, E. J. P. & MANN, J. A., 1998. Analyzing maps of dispersal around a single focus. Environmental and Ecological Statistics, 5:317-344.         

KULLDORF, M., 1997. A spatial scan statistic. Communications in Statistics - Theory and Methods, 26:1481-1496.         

KULLDORF, M.; FEUER, E. J.; MILLER, B. A. & FREEDMAN, L. S., 1997. Breast cancer clusters in the northeast United States: A geographic analysis. American Journal of Epidemiology, 146:161-170.         

KULLDORF, M. & HJALMARS, U., 1999. The Knox method and other tests for space-time interaction. Biometrics, 55:544-552.         

KULLDORF, M. & NAGARWALLA, N., 1995. Spatial disease clusters: Detection and inference. Statistics in Medicine, 14:799-810.         

KYRIAKIDIS, P. C. & JOURNEL, A. G., 1999. Geostatistical space-time models: A review. Mathematical Geology, 31:651-684.         

LANGFORD, I. & LEWIS, T., 1998. Outliers in multi-level models. Journal of the Royal Statistical Society, Series A, 101:121-160.         

LAWSON, A., 1993. On the analysis of mortality events around a prespecified fixed point. Journal of the Royal Statistical Society, Series A, 156:363-377.         

LAWSON, A., 1995. Markov Chain Monte Carlo methods for putative polution source problems in environmental epidemiology. Statistics in Medicine, 14:2473-2486.         

LAWSON, A.; BIGGERI, A.; BÖHNING, D.; LESAFFRE, E.; VIEL, J.-F. & BERTOLLINI R., 1999a. Disease Mapping and Risk Assessment for Public Health. Chichester: Wiley.         

LAWSON, A.; BIGGERI, A. & DREASSA, E., 1999b. Edge effects in disease mapping. In: Disease Mapping and Risk Assessment for Public Health (A. Lawson, A. Biggeri, D. Böhning, E.Lesaffre, J.-F. Viel & R. Bertollini ed.), pp. 85-97, Chichester: Wiley.         

LAWSON, A. & CLARK, A., 1999. Markov Chain Monte Carlo methods for clustering in case event and count data in spatial epidemiology. In: Statistics and Epidemiology: Environment and Health (E. Halloran & J. Greenhouse, ed.), pp. 151-163, New York: Springer-Verlag.         

LAWSON, A. & VIEL, J.-F., 1995. Tests for directional space-time interaction in epidemiological studies. Statistics in Medicine, 14:2383-2392.         

LAWSON, A. & WALLER, L., 1996. A review of point pattern methods for spatial modelling of events around sources of pollution. Environmetrics, 7:471-488.         

MANTEL, N., 1967. The detection of disease clustering and a generalised regression approach. Cancer Research, 27:209-220.         

MARTUZZI, M. & ELLIOTT, P., 1996. Empirical Bayes estimation of small area prevalence in non-rare conditions. Statistics in Medicine, 15:1867-1873.         

MOLLIE, A., 1995. Bayesian mapping of disease. In: Markov Chain Monte Carlo in Practice (W. R. Gilks, S. Richardson & D. J. Spiegelhalter, ed.), pp. 359-379, London: Chapman & Hall.         

MULLER, H. G.; STADTMULLER, U. & TABNAK, F., 1997. Spatial smoothing of geographically aggregated data, with application to the construction of incidence maps. Journal of the American Statistical Association, 92:61-71.         

NEUTRA, R. R., 1990. Counterpoint from a cluster buster. American Journal of Epidemiology, 132 (Sup.):1-8.         

NEUTRA, R. R., 1999. Computer geographic analysis: A commentray on its use and misuse in public health. In: Disease Mapping and Risk Assessment for Public Health (A. Lawson, A. Biggeri, D. Böhning, E. Lesaffre, J.-F. Viel, & R. Bertollini, ed.), pp. 311-319, Chichester: Wiley.         

ODEN, N., 1995. Adjusting Moran's I for population density. Statistics in Medicine, 14:17-26.         

OLSEN, S.; MARTUZZI, M. & ELLIOTT, P., 1996. Cluster analysis and disease mapping - Why, when, how? A step by step guide. BMJ, 313:863-865.         

OPPENSHAW, S., 1991. A new approach to the detection and validation of cancer clusters: A review of opportunities, progress and problems. In: Statistics in Medicine (F. Dunstan & J. Pickles, ed.), pp. 49-63, Oxford: Clarendon Press.         

PIEGORSCH, W. W.; SMITH, E. P.; EDWARDS, D. & SMITH, R. L., 1998. Statistical advances in environmental science. Statistical Science, 13:186-208.         

PLUMMER, M. & CLAYTON, D., 1996. Estimation of population exposure in ecological studies. Journal of the Royal Statistical Society, Series B, 58: 113-126.         

POTTHOFF, R. F. & WHITTINGHILL, M., 1966. Testing for Homogeneity. Biometrika, 53:167-190.         

PRENTICE, R. & SHEPPARD, L., 1995. Aggregate data studies of disease risk factors. Biometrika, 82:113-125.         

RICHARDSON, S. & GREEN, P., 1997. On Bayesian analysis of mixtures with an unknown number of components. Journal of the Royal Statistical Society, Series B, 59:731-792.         

RICHARDSON, S.; GUIHENNEUC, C. & LASSERRE, V., 1992. Spatial linear models with autocorrelated error structure. Journal of the Royal Statistical Society, Series D, 41:539-557.         

RUSHTON, G.; KRISHNAMURTHY, R.; KRISHNAMURTI, D.; LOLONIS, P. & SONG, H., 1996. The spatial relationship between infant mortality and birth defect rates in a US city. Statistics in Medicine, 15:1907-1919.         

SCHALTTMANN, P. & BÖHNING, D., 1993. Mixture models and disease mapping. Statistics in Medicine, 12:1943-1950.         

SCHALTTMANN, P.; BÖHNING, D. & DIETZ, E., 1996. Covariate adjusted mixture models with the program DismapWin. Statistics in Medicine, 15:919-929.         

SCHRODER, M.; REHRAUER, H.; SEIDEL, K. & DATCU, M., 1998. Spatial information retrieval from remote - sensing images - Part II: Gibbs-Markov random fields. IEEE Transations on Geoscience and Remote Sensing, 36:1446-1455.         

SPIEGELHALTER, D.; THOMAS, A.; BEST, N. & GILKS, W., 1997. BUGS: Bayesian Inference Using Gibbs Sampling. Cambridge: Medical Research Council Biostatistics Unit.         

SPIEGELHALTER, D., 1998. Bayesian graphical modelling: A case study in monitoring health outcomes. Journal of the Royal Statistical Society, Series C, 47:115-133.         

SPSS INCORPORATION, 1997. SPSS for Windows. Statistical Package for the Social Sciences. Release 8.0. Chicago: SPSS Inc.         

STEIN, A.; VanGROENIGEN, J. W.; JEGER, M. J. & HOOSBEEK, M. R., 1998a. Space-time statistics for environmental and agricultural related phenomena. Environmental and Ecological Statistics, 5:155-172.         

STEIN, A.; BASTIAANSSEN, W. G. M.; DeBRUIN, S.; CRACKNELL, A. P.; CURRAN, P. J., FABBRI, A. G.; GORTE, B. G. H.; VanGROENIGEN, J. W.; VanderMEER, F. D. & SALDANA, A., 1998b. Integrating spatial statistics and remote sensing. International Journal of Remote Sensing, 19:1793-1814.         

STONE, R., 1988. Investigations of excess environmental risks around putative sources: Statistical problems and a proposed test. Statistics in Medicine, 7:649-660.         

TANGO, T., 1995. A class of test for detecting "general" and "focussed" clustering of rare diseases. Statistics in Medicine, 14:2323-2334.         

THOMSON, M. C.; CONNOR, S. J.; DALESSANDRO, U.; ROWLINGSON, B.; DIGGLE, P.; CRESSWELL, M. & GREENWOOD, B., 1999. Predicting malaria infection in Gambian children from satellite data and bed net use surveys: The importance of spatial correlation in the interpretation of results. American Journal of Tropical Medicine and Hygiene, 61:2-8.         

TJELMELAND, H. & BESAG, J., 1998. Markov random fields with higher-order interactions. Scandinavian Journal of Statistics, 25:415-433.         

TURNBULL, B.; IWANO, E.; BURNETT, W.; HOWE, H. & CLARK, L., 1990. Monitoring for clusters of disease: Application to Leukaemia incidence in upstate New York. American Journal of Epidemiology, 132:136-143.         

UNWIN, A. & UNWIN, D., 1998. Exploratory spatial data analysis with local statistics. Journal of the Royal Statistical Society, Series D, 47:415-421.         

VENABLES, W. N. & RIPLEY, B. D., 1994. Modern Applied Statistics with S-Plus. Berlin: Springer-Verlag.         

WALLER, L.; CARLIN, B.; XIA, H. & GELFAND, A., 1997. Hierarchical spatio-temporal mapping of disease rates. Journal of the American Statistical Association, 92:607-617.         

WALLER, L. & LAWSON, A., 1995. The power of focussed tests to detect disease clustering. Statistics in Medicine, 14:2291-2308.         

WALLER, L. & TURNBULL, B., 1993. The effect of scale on tests for disease clustering. Statistics in Medicine, 12:1869-1884.         

WALTER, S., 1993a. Assessing spatial pattern in disease rates. Statistics in Medicine, 12:1885-1894.         

WALTER, S., 1993b. Visual and statistical assessment of spatial clustering in mapped data. Statistics in Medicine, 12:1275-1291.         

WALTER, S., 1994. A simple test for spatial pattern in regional health data. Statistics in Medicine, 13: 1037-1044.         

WEBSTER, R.; OLIVER, M.; MUIR, K. & MANN, J., 1994. Kriging the local risk of a rare disease from a register of diagnoses. Geographical Analysis, 26:168-185.         

WEIR, I. S. & PETTITT, A. N., 1999. Spatial modelling for binary data using a hidden conditional autoregressive Gaussian process: A multivariate extension of the probit model. Statistics and Computing, 9:77-86.         

WHITTEMORE, A.; FRIEND, N.; BROWN, B. & HOLLY, E., 1987. A test to detect clusters of disease. Biometrika, 74:631-635.         

WIKLE, C. K.; BERLINER, L. M. & CRESSIE, N., 1998. Hierarchical Bayesian space-time models. Environmental and Ecological Statistics, 5:117-154.         

WILHELM, A. & STECK, R., 1998. Exploring spatial data by using interactive graphics and local statistics. Journal of the Royal Statistical Society, Series D, 47:423-430.         

WOLPERT, R. L. & ICKSTADT, K., 1998. Poisson/gamma random field models for spatial statistics. Biometrika, 85:251-267.         

XIA, H.; CARLIN, B. P. & WALLER, L. A., 1997. Hierarchical models for mapping Ohio lung cancer rates. Environmetrics, 8:107-120.         

YASUI, Y. & LELE, S., 1997. A regression method for spatial disease rates: An estimating function approach. Journal of the American Statistical Association, 92:21-32.